题目内容
14.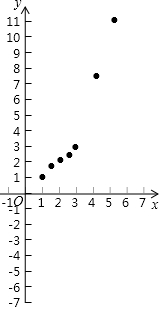 有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.
有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.(1)先从简单情况开始探究:
①当函数y=$\frac{1}{2}$(x-1)+x时,y随x增大而增大(填“增大”或“减小”);
②当函数y=$\frac{1}{2}$(x-1)(x-2)+x时,它的图象与直线y=x的交点坐标为(1,1),(2,2);
(2)当函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x时,
下表为其y与x的几组对应值.
| x | … | -$\frac{1}{2}$ | 0 | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | $\frac{9}{2}$ | … |
| y | … | -$\frac{113}{16}$ | -3 | 1 | $\frac{27}{16}$ | 2 | $\frac{37}{16}$ | 3 | 7 | $\frac{177}{16}$ | … |
②根据画出的函数图象,写出该函数的一条性质:y随x的增大而增大.
分析 (1)①根据一次函数的性质得出即可;
②求出组成的方程组的解,即可得出答案;
(2)①把各个点连接即可;②根据图象写出一个符合的信息即可.
解答 解:(1)①∵y=$\frac{1}{2}$(x-1)+x=$\frac{3}{2}$x-$\frac{1}{2}$,
k=$\frac{3}{2}$>0,
∴y随x增大而增大,
故答案为:增大;
②解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}(x-1)(x-2)+x}\\{y=x}\end{array}\right.$得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=2}\end{array}\right.$,
所以两函数的交点坐标为(1,1),(2,2),
故答案为:(1,1),(2,2);
(2)①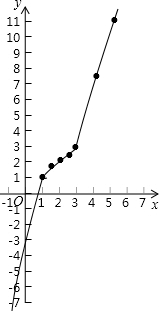
②该函数的性质:
①y随x的增大而增大;
②函数的图象经过第一、三、四象限;
③函数的图象与x轴y轴各有一个交点等,
故答案为:y随x的增大而增大.
点评 本题考查了一次函数的性质,二次函数的性质等知识点,能够根据图象得出正确信息是解此题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
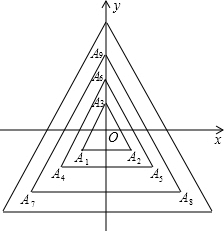 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2017的坐标是(-673,-673).
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4、…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则A2017的坐标是(-673,-673). 己知在梯形ABCD中,AB∥DC,∠A=∠B=45°,AB=4,AD=$\sqrt{2}$,则此梯形的面积是3.
己知在梯形ABCD中,AB∥DC,∠A=∠B=45°,AB=4,AD=$\sqrt{2}$,则此梯形的面积是3.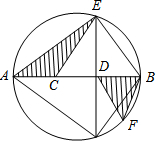 如图,半径为3cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连接AE,BF,则图中两个阴影部分的面积为$\frac{3\sqrt{11}}{2}$.
如图,半径为3cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连接AE,BF,则图中两个阴影部分的面积为$\frac{3\sqrt{11}}{2}$.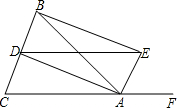 如图,在△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAF的平分线,BE⊥AE
如图,在△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAF的平分线,BE⊥AE