题目内容
20.在Rt△ABC中,CD是斜边AB上的高,若AC=$\sqrt{2}$,BC=1,则BD的长为( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 首先根据勾股定理求出AB的长度,然后根据Rt△ABC面积的不同计算公式求出CD的长度,在Rt△CDB中用勾股定理求出BD的长度.
解答 解:在Rt△ABC中,CD是斜边AB上的高,
∵AC=$\sqrt{2}$,BC=1,
∴($\sqrt{2}$)2+12=AB2,
解得:AB=$\sqrt{3}$,
∴Rt△ABC的面积为:$\frac{1}{2}$×AC×BC=$\frac{1}{2}$AB•CD,
∴CD=$\frac{\sqrt{6}}{3}$.
在Rt△CDB中,BD2=BC2-CD2,
解得:BD=$\frac{\sqrt{3}}{3}$.
故选B.
点评 本题主要考查了勾股定理,三角形的面积,在直角三角形中斜边的平方等于两直角边的平方和.另外在求一边上的高时可以利用面积的不同计算公式求出此高的长度.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图是一个全由棱长为1的正方体堆积而成的几何体的俯视图,俯视图上的数字表示此位置的小立方块的个数,求这个几何体的表面积.
如图是一个全由棱长为1的正方体堆积而成的几何体的俯视图,俯视图上的数字表示此位置的小立方块的个数,求这个几何体的表面积.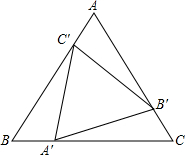 已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形.
已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形.