题目内容
9.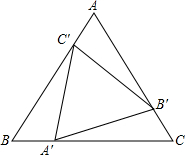 已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形.
已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形.
分析 由△ABC是等边三角形,AC′=BA′=CB′,易证得△AC′B′≌△BA′C′,即可得C′B′=A′C′,同理可得C′B′=B′A′,即可证得△A′B′C′是等边三角形.
解答 证明:∵△ABC是等边三角形,
∴AB=BC=AC,
∵AC′=BA′=CB′,
∴AB′=BC′,
在△AC′B′和△BA′C′中,
$\left\{\begin{array}{l}{AC′=BA′}\\{∠A=∠B}\\{AB′=BC′}\end{array}\right.$,
∴△AC′B′≌△BA′C′(SAS),
∴C′B′=A′C′,
同理B′C′=A′B′,
∴C′B′=A′C′=A′B′,
∴△A′B′C′是等边三角形.
点评 此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
19.如图是小明一天上学时看到一棵树的影子的俯视图,将它们按时间先后顺序进行排列,正确的是( )


| A. | ④①②③ | B. | ④③②① | C. | ④②①③ | D. | ③①②④ |
20.在Rt△ABC中,CD是斜边AB上的高,若AC=$\sqrt{2}$,BC=1,则BD的长为( )
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
19.一个水分子的质量大约为3×10-26kg,一位学生饮用了180g水,他大约喝下去的水分子个数约为( )
| A. | 6×1023 | B. | 180×6×1023 | C. | 18×6×1023 | D. | 6×1024 |
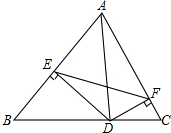 △ABC中,AD⊥BC于点D,DE⊥AC于E,DF⊥AB于点F,求证:∠AFE=∠B.
△ABC中,AD⊥BC于点D,DE⊥AC于E,DF⊥AB于点F,求证:∠AFE=∠B. 如图,AB=AC,BD=CD.
如图,AB=AC,BD=CD. 如图,已知AD是△ABC的角平分线,且AC=AB+BD,∠C=30°,求∠BAC的度数.
如图,已知AD是△ABC的角平分线,且AC=AB+BD,∠C=30°,求∠BAC的度数. 如图,在△ABC中,∠CAB的平分线AD与BC垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC,交AC的延长线于点N,求证:BM=CN.
如图,在△ABC中,∠CAB的平分线AD与BC垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC,交AC的延长线于点N,求证:BM=CN.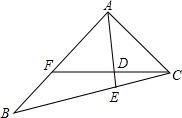 如图,△ABC中,点F在边AB上,AC=AF,AD⊥CF于点D,AD的延长线交BC于点E,求证:$\frac{BE}{EC}$=$\frac{AB}{AF}$.
如图,△ABC中,点F在边AB上,AC=AF,AD⊥CF于点D,AD的延长线交BC于点E,求证:$\frac{BE}{EC}$=$\frac{AB}{AF}$.