题目内容
若抛物线y=（2-m）（x-m）2+m的顶点在第一象限，且图象与x轴没有交点，则m的取值范围 ．
考点：抛物线与x轴的交点
专题：
分析：直接利用顶点形式结合得出顶点在第一象限，且图象与x轴没有交点，得出图象开口向上，且m＞0，即可求出答案．
解答：解：∵抛物线y=（2-m）（x-m）2+m的顶点在第一象限，且图象与x轴没有交点，
∴图象开口向上，顶点坐标为：（m，m），则m＞0，
故2-m＞0，
解得：0＜m＜2．
故答案为：0＜m＜2．
∴图象开口向上，顶点坐标为：（m，m），则m＞0，
故2-m＞0，
解得：0＜m＜2．
故答案为：0＜m＜2．
点评：此题主要考查了抛物线与x轴交点，得出抛物线开口方向是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，抛物线y=-x2+2x的顶点为M，点P为第四象限的抛物线上一点，以PM为直径的⊙O′恰好以过点O，求P点的坐标．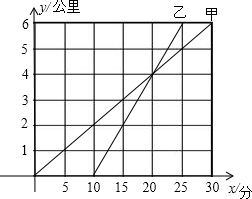
甲骑自行车、乙骑摩托车沿相同路线由A地到B地，如图是行驶过程中路程y与时间x的关系的图象．根据图象，回答下列问题：