题目内容
某果园有100棵苹果树,平均每棵树可结660个苹果,根据经验估计,在这个果园里每多种一棵树,平均每棵树就会少结6个苹果,则果园里增 棵苹果树,所结苹果的总数最多.
考点:二次函数的应用
专题:应用题
分析:设果园里增x棵苹果树,所结苹果的总数为y,则果园里有(100+x)棵苹果树,而平均每棵树可结的苹果为(660-6x)个,所以y=(100+x)(660-6x),然后配方得到顶点式,再利用二次函数的最值问题解决问题.
解答:解:设果园里增x棵苹果树,所结苹果的总数为y,
根据题意得y=(100+x)(660-6x)
=-6x2+60x+66000
=-6(x-5)2+66150,
∵a=-6,
∴当x=5时,y有最大值66150,
即果园里增5棵苹果树,所结苹果的总数最多.
故答案为5.
根据题意得y=(100+x)(660-6x)
=-6x2+60x+66000
=-6(x-5)2+66150,
∵a=-6,
∴当x=5时,y有最大值66150,
即果园里增5棵苹果树,所结苹果的总数最多.
故答案为5.
点评:本题考查了二次函数的实际应用:利用二次函数解决利润问题,在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.

练习册系列答案
相关题目
以下列各组数据为三角形的三边长,能构成直角三角形的是( )
| A、2cm,3cm,4cm |
| B、3cm,5cm,6cm |
| C、2cm,6cm,40cm |
| D、6cm,8cm,10cm |
 如图,AB∥CD,∠A=45°,且OC=OE,求∠C的度数.
如图,AB∥CD,∠A=45°,且OC=OE,求∠C的度数. 如图,在△ABC中,若BD:DC=CE:EA=2:1,AD和BE交于F,求AF:FD.
如图,在△ABC中,若BD:DC=CE:EA=2:1,AD和BE交于F,求AF:FD.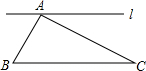 如图,已知∠A=90°,∠C=30°,AB=2,过点A的直线l与BC平行.若D是l上的一点,且BD=DC,求AD两点间的距离.
如图,已知∠A=90°,∠C=30°,AB=2,过点A的直线l与BC平行.若D是l上的一点,且BD=DC,求AD两点间的距离.