题目内容
9.解方程:x(x-1)=2.有学生给出如下解法:
∵x(x-1)=2=1×2=(-1)×(-2),
∴$\left\{\begin{array}{l}x=1\\ x-1=2\end{array}\right.$或$\left\{\begin{array}{l}x=2\\ x-1=1\end{array}\right.$或$\left\{\begin{array}{l}x=-1\\ x-1=-2\end{array}\right.$或$\left\{\begin{array}{l}x=-2\\ x-1=-1.\end{array}\right.$
解上面第一、四方程组,无解;解第二、三方程组,得 x=2或x=-1
∴x=2或x=1
请问:这个解法对吗?试说明你的理由.
分析 首先解出一元二次方程x(x-1)=2的两个解,然后对该学生的解法作出判断.
解答 解:答案一:
x(x-1)=2,解得x=2或1,
对于这个特定的已知方程,解法是对的.
理由是:一元二次方程有根的话,只能有两个根,此学生已经将两个根都求出来了,所以对;
答案二:
解法不严密,方法不具有一般性,
理由是:为何不可以2=3×$\frac{2}{3}$等,得到其它的方程组?此学生的方法只是巧合了,求对了方程的根.
点评 本题主要考查了因式分解法解一元二次方程的知识,解答本题的关键是掌握因式分解法解方程的步骤,此题解答完全凑巧,难度不大.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
4.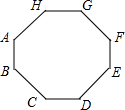 如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
 如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )
如图,八边形ABCDEFGH中,AB=CD=EF=GH=1,BC=DE=FG=HA=$\sqrt{2}$,∠A=∠B=∠C=∠D=∠E=∠F=∠H=135°,则这个八边形的面积等于( )| A. | 7 | B. | 8 | C. | 9 | D. | 14$\sqrt{2}$ |
1.在平面直角坐标系中,点A(-2,3)关于x轴对称的对称点B的坐标为( )
| A. | (2,-3) | B. | (-2,-3) | C. | (-2,3) | D. | (2,3) |
 如图,∠BAC=30°,点P时∠BAC的平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PM=8,则PD=4.
如图,∠BAC=30°,点P时∠BAC的平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PM=8,则PD=4.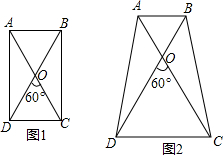 已知:在四边形ABCD中,AC=BD,AC与BD交于点O,∠DOC=60度.
已知:在四边形ABCD中,AC=BD,AC与BD交于点O,∠DOC=60度.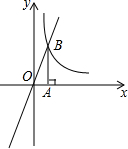 如图,正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B.若k取1,2,3,…,10,对应的Rt△AOB的面积分别为S1,S2,…,S10,则S1+S2+…S10=$\frac{55}{2}$.
如图,正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B.若k取1,2,3,…,10,对应的Rt△AOB的面积分别为S1,S2,…,S10,则S1+S2+…S10=$\frac{55}{2}$.
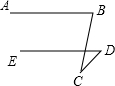 如图所示,AB∥DE,如果点C在AB与ED之外,其他条件不变,那么∠ABC、∠CDE与∠BCD之间会有怎样的数量关系,请证明,你还能就本题作出什么新的猜想?
如图所示,AB∥DE,如果点C在AB与ED之外,其他条件不变,那么∠ABC、∠CDE与∠BCD之间会有怎样的数量关系,请证明,你还能就本题作出什么新的猜想?