题目内容
14.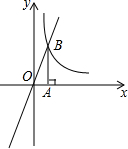 如图,正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B.若k取1,2,3,…,10,对应的Rt△AOB的面积分别为S1,S2,…,S10,则S1+S2+…S10=$\frac{55}{2}$.
如图,正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B.若k取1,2,3,…,10,对应的Rt△AOB的面积分别为S1,S2,…,S10,则S1+S2+…S10=$\frac{55}{2}$.
分析 根据正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B,求出一般形式Sk=$\frac{1}{2}$×3×$\frac{k}{3}$,再代入即可求解.
解答 解:根据正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$的图象交于点B,
∴x2=$\frac{k}{3}$,
∴SK=$\frac{1}{2}$×3×$\frac{k}{3}$,
∴S1+S2+…+S10
=$\frac{1}{2}$×3×$\frac{1}{3}$+$\frac{1}{2}$×3×$\frac{2}{3}$+…+$\frac{1}{2}$×3×$\frac{10}{3}$
=$\frac{1}{2}$(1+2+3+…+10)
=$\frac{55}{2}$.
故答案为:$\frac{55}{2}$.
点评 本题考查了反比例函数与一次函数的交点,属于基础题,关键是求出一般形式后再进行代入求解.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
4.下列四组数:①5,12,13;②7,24,25;③3a,4a,5a(a>0);④32,42,52.⑤$\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$,其中可以构成直角三角形的边长有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
5. 明明家今年1~5月份的用电量情况如图所示,则相邻两个月用电量变化最大的是( )
明明家今年1~5月份的用电量情况如图所示,则相邻两个月用电量变化最大的是( )
 明明家今年1~5月份的用电量情况如图所示,则相邻两个月用电量变化最大的是( )
明明家今年1~5月份的用电量情况如图所示,则相邻两个月用电量变化最大的是( )| A. | 1月至2月 | B. | 2月至3月 | C. | 3月至4月 | D. | 4月至5月 |
2.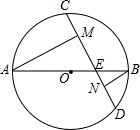 如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )
如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )
 如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )
如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | $\sqrt{2}$ |
19.为促进义务教育办学条件均衡,某市投入260万元资金为部分学校添置实验仪器,260万用科学记数法表示为( )
| A. | 260×103 | B. | 26×105 | C. | 2.6×105 | D. | 2.6×106 |
3.设x1、x2是一元二次方程x2+x-3=0的两根,则x13-4x22+15等于( )
| A. | -4 | B. | 8 | C. | 6 | D. | 0 |
 如图,在平行四边形ABCD中,AB=2,BC=4,AC的垂直平分线交AD于点E,则△CDE的周长为6.
如图,在平行四边形ABCD中,AB=2,BC=4,AC的垂直平分线交AD于点E,则△CDE的周长为6.