题目内容

19．若关于x的一元二次方程kx2-6x+9=0有两个不相等的实数根，则k的取值范围k＜1且k≠0．

分析 因为关于x的一元二次方程kx2-6x+9=0有两个不相等的实数根，所以k≠0且△=b2-4ac＞0，建立关于k的不等式组，解得k的取值范围即可．

解答 解：∵关于x的一元二次方程kx2-6x+9=0有两个不相等的实数根，
∴k≠0，且△=b2-4ac=36-36k＞0，
解得k＜1且k≠0．
故答案为k＜1且k≠0．

点评 本题考查了一元二次方程根的判别式的应用．切记不要忽略一元二次方程二次项系数不为零这一隐含条件．
总结：一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．

练习册系列答案
相关题目
9．计算
（1）（-2）-（-5）+（-9）-（-7）
（2）-24×（-$\frac{1}{2}$+$\frac{3}{4}$-$\frac{1}{3}$）
（3）（-6）×8-（-2）3+（-4）2×5
（4）（+3$\frac{2}{5}$）+（-2$\frac{7}{8}$）+（-3$\frac{5}{12}$）+（-1$\frac{1}{8}$）+（+5$\frac{3}{5}$）+（+3$\frac{5}{12}$）
（5）-14-（1-0.5）×$\frac{1}{3}$×[10-（-2）2]-（-1）3．
10．甲、乙两站间的路程为520千米，甲车每小时行80千米，乙车每小时行60千米，两车同时从甲、乙两站开出，相向而行，两车开出一段时间后，甲车因故停了30分钟，再继续前进与乙相遇，则相遇时乙车走了多少小时？
7．已知反比例函数y=-$\frac{{a}^{2}+1}{x}$的图象上有三点A1（x1，y1），A2（x2，y2），A3（x3，y3），已知x1＜x2＜0＜x3，则下列各式中，正确的是（　　）
A．y1＜y2＜y3B．y3＜y2＜y1C．y2＜y1＜y3D．y3＜y1＜y2
14．一组邻边相等的矩形是正方形．√．（判断对错）
4．下列四组数：①5，12，13；②7，24，25；③3a，4a，5a（a＞0）；④32，42，52．⑤$\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$，其中可以构成直角三角形的边长有（　　）
A．1组B．2组C．3组D．4组
11．观察下列各式及验证过程：
$\sqrt{\frac{1}{2}-\frac{1}{3}}$=$\frac{1}{2}$$\sqrt{\frac{2}{3}}$，验证：$\sqrt{\frac{1}{2}-\frac{1}{3}}$=$\sqrt{\frac{1}{2×3}}$=$\sqrt{\frac{2}{{2}^{2}×3}}$=$\frac{1}{2}$$\sqrt{\frac{2}{3}}$；
$\sqrt{\frac{1}{2}（\frac{1}{3}-\frac{1}{4}）}$=$\frac{1}{3}$$\sqrt{\frac{3}{8}}$，验证：$\sqrt{\frac{1}{2}（\frac{1}{3}-\frac{1}{4}）}$=$\sqrt{\frac{1}{2×3×4}}$=$\sqrt{\frac{3}{2×{3}^{2}×4}}$=$\frac{1}{3}$$\sqrt{\frac{3}{8}}$；
$\sqrt{\frac{1}{3}（\frac{1}{4}-\frac{1}{5}）}$=$\frac{1}{4}$$\sqrt{\frac{4}{15}}$，验证：$\sqrt{\frac{1}{3}（\frac{1}{4}-\frac{1}{5}）}$=$\sqrt{\frac{1}{3×4×5}}$=$\sqrt{\frac{4}{3×{4}^{2}×5}}$=$\frac{1}{4}$$\sqrt{\frac{4}{15}}$；
$\sqrt{\frac{1}{4}（\frac{1}{5}-\frac{1}{6}）}$=$\frac{1}{5}$$\sqrt{\frac{5}{24}}$，验证：$\sqrt{\frac{1}{4}（\frac{1}{5}-\frac{1}{6}）}$=$\sqrt{\frac{1}{4×5×6}}$=$\sqrt{\frac{5}{4×{5}^{2}×6}}$=$\frac{1}{5}$$\sqrt{\frac{5}{24}}$；
（1）按照上述四个等式及其验证过程的基本思路，猜想$\sqrt{\frac{1}{5}（\frac{1}{6}-\frac{1}{7}）}$的变形结果并进行验证；
（2）针对上述各式反映的规律，写出用n（n≥1为整数）表示的等式．
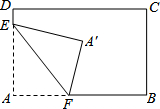8．我们知道，长方形的四个角都是直角．现将长方形纸片ABCD的一角A折叠到点A′的位置（如图所示），折痕为EF，如果∠A′FB=76°，那么∠AEF=38°°．
9．解方程：x（x-1）=2．
有学生给出如下解法：
∵x（x-1）=2=1×2=（-1）×（-2），
∴$\left\{\begin{array}{l}x=1\\ x-1=2\end{array}\right.$或$\left\{\begin{array}{l}x=2\\ x-1=1\end{array}\right.$或$\left\{\begin{array}{l}x=-1\\ x-1=-2\end{array}\right.$或$\left\{\begin{array}{l}x=-2\\ x-1=-1.\end{array}\right.$
解上面第一、四方程组，无解；解第二、三方程组，得 x=2或x=-1
∴x=2或x=1
请问：这个解法对吗？试说明你的理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网