题目内容
5.已知菱形的两条对角线的长分别为12$\sqrt{3}$cm和12cm,则此菱形的最大内角为120度.分析 根据菱形的性质可得AC⊥DB,AO=CO=$\frac{1}{2}$AC=6cm,BO=DO=$\frac{1}{2}$DB=6$\sqrt{3}$cm,∠BAD=2∠BAC,利用三角形函数计算出∠ABO=30°,进而可得∠BAC的度数,然后可得答案.
解答 解: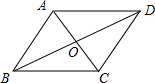 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AC⊥DB,AO=CO=$\frac{1}{2}$AC=6cm,BO=DO=$\frac{1}{2}$DB=6$\sqrt{3}$cm,∠BAD=2∠BAC,
∵tan∠ABO=$\frac{AO}{BO}$=$\frac{6}{6\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠ABO=30°,
∴∠BAC=60°,
∴∠BAD=120°,
故答案为:120.
点评 此题主要考查了菱形的性质,关键是掌握①菱形具有平行四边形的一切性质; ②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 如图,在菱形ABCD中,点F是对角线BD上一点,连站AF交BC于点B,连接CF.∠AEB与∠DCF在数量上有什么关系,并证明你的猜想.
如图,在菱形ABCD中,点F是对角线BD上一点,连站AF交BC于点B,连接CF.∠AEB与∠DCF在数量上有什么关系,并证明你的猜想. 如图,在?ABCD中,E是BC边上一点,连结DE,使得DE=AD,作∠DAF=∠CDE.
如图,在?ABCD中,E是BC边上一点,连结DE,使得DE=AD,作∠DAF=∠CDE. 如图,在△ABC中,D、E分别是边AB和AC上的点,将△ABC纸片沿DE折叠,点A落到点F的位置.如果DF∥BC,∠B=60°,∠CEF=40°,则∠F=80°.
如图,在△ABC中,D、E分别是边AB和AC上的点,将△ABC纸片沿DE折叠,点A落到点F的位置.如果DF∥BC,∠B=60°,∠CEF=40°,则∠F=80°. 如图,已知四边形ABCD是平行四边形.
如图,已知四边形ABCD是平行四边形. 在如图所示的4×3网格中,每个小正方形的边长均为1,正方形的顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.
在如图所示的4×3网格中,每个小正方形的边长均为1,正方形的顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上. 如图,正方形网格中的每个小正方形边长都是1,每个小正方形的顶点叫格点,点A、B、C均在格点上.
如图,正方形网格中的每个小正方形边长都是1,每个小正方形的顶点叫格点,点A、B、C均在格点上.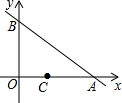 如图,直线y=-x+3交x轴于点A,交y轴于点B,点C的坐标为(1,0).
如图,直线y=-x+3交x轴于点A,交y轴于点B,点C的坐标为(1,0).