Question

20．如图，已知四边形ABCD是平行四边形．
（1）用直尺和圆规作出∠ABC的平分线BE，BE交CD的延长线于点E，交AD于点F；（保留作图痕迹，不写作法）
（2）若AB=2cm，BC=3cm，BE=5cm，求BF的长．

Answer 1

分析 （1）利用尺规作出∠ABC的平分线即可．
（2）先证明AB=AF=2，BC=CE=3，再根据AB∥DE，推出$\frac{AB}{DE}$=$\frac{BF}{EF}$，列出方程即可解决问题．

解答 解：（1）答案如图所示．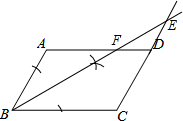

（2）∵四边形ABCD是平行四边形，
∴AB=CD=2，BC=AD=3，AD∥BC，AB∥CD，
∵BE平分∠ABC，
∴∠ABF=∠CBE，∠CBE=∠AFB，
∴∠ABF=∠AFB，
∴AB=AF=2，同理BC=CE=3，设BF=x，
∵AB∥DE，
∴$\frac{AB}{DE}$=$\frac{BF}{EF}$，
∴$\frac{2}{1}$=$\frac{x}{5-x}$，
∴x=$\frac{10}{3}$．

点评 本题考查平行四边形的性质、角平分线的作法、等腰三角形的判定和性质等知识，解题的关键是利用等腰三角形的性质解决问题，学会设未知数构建方程的思想解决问题，属于中考常考题型．