题目内容
1．
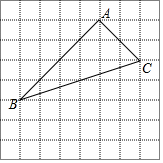如图，在边长为1的小正方形组成的方格纸中，有一个以格点为顶点的△ABC．（1）试根据三角形三边关系，判断△ABC的形状；
（2）在方格纸中利用直尺分别画出AB、BC的垂直平分线（要求描出关键格点），交点为O．问点O到△ABC三个顶点的距离相等吗？说明理由．
分析 （1）根据勾股定理求得该三角形的三条边的长度，然后结合勾股定理的逆定理判定该三角形为直角三角形；
（2）根据题意得到图形，由此可以得到点O位于斜边BC上．
解答 
解：（1）如图所示，AB2=42+42=32，BC2=62+22=40，AC2=22+22=8，
所以AB2+AC2=BC2．
所以△ABC是直角三角形；
（2）如图所示，点O是△ABC的外心，且在斜边BC上．
点评 本题考查了勾股定理，勾股定理逆定理，线段垂直平分线的性质．注意：勾股定理应用于直角三角形中．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如表所示：
（1）顶点坐标为（2，0）；
（2）若将此图象沿x轴向右平移3个单位，请写出平移后图象所对应的函数关系式：y=（x-5）2；
（3）设点P1（m，y1）、P2（m+1，y2）、P3（m+2，y3）都在二次函数y=ax2+bx+c的图象上，问：当m＜-3时，y1、y2、y3的值一定能作为同一个三角形三边的长吗？为什么？
| x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | 9 | … |
（2）若将此图象沿x轴向右平移3个单位，请写出平移后图象所对应的函数关系式：y=（x-5）2；
（3）设点P1（m，y1）、P2（m+1，y2）、P3（m+2，y3）都在二次函数y=ax2+bx+c的图象上，问：当m＜-3时，y1、y2、y3的值一定能作为同一个三角形三边的长吗？为什么？
一般地，点C把线段AB分成两条线段AC和BC，如果$\frac{AC}{AB}$=$\frac{BC}{AC}$，那么称线段AB被点C黄金分割，点C叫做线段AB的黄金分割点，AC与AB的比叫做黄金比．请计算黄金比．