题目内容
16. 一般地,点C把线段AB分成两条线段AC和BC,如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.请计算黄金比.
一般地,点C把线段AB分成两条线段AC和BC,如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.请计算黄金比.
分析 设AB=1,AC=x,根据黄金分割的概念列出比例式,得到一元二次方程,解方程得到答案.
解答 解:设AB=1,AC=x,则BC=1-x,
由$\frac{AC}{AB}$=$\frac{BC}{AC}$,得AC2=AB•CB,
则x2=1×(1-x)
整理得;x2+x-1=0,
解得:x1=$\frac{\sqrt{5}-1}{2}$,x2=$\frac{-\sqrt{5}-1}{2}$(不合题意,舍去).
故黄金比为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查的是黄金分割,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键,注意方程思想的正确运用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
4.下列各组数是勾股数的是( )
| A. | 32,42,52 | B. | 1.5,2,2.5 | C. | 6,8,10 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
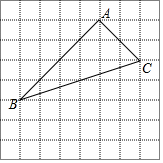 如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.
如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC. 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题: