题目内容
13.如图1,已知△ABC中,∠BAC=90°,AB=AC,点P为直线BC上一动点,分别过B、C作BD⊥AP于D,CE⊥AP于E.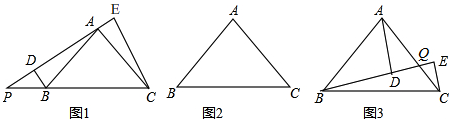
(1)若点P为CB延长线上一点,则线段BD、CE、DE是否存在某种确定的数量关系?写出你的结论并证明.
(2)如图2若点P为线段BC上一点,则线段BD、CE、DE是否存在某种确定的数量关系?画图并直接写出你的结论DE=BD-CE(不证明).
(3)如图3,若点Q为线段AC上一点,分别过A、C作AD⊥BQ于D,CE⊥BQ于E,则线段AD、BD、CE是否存在某种确定的数量关系?直接写出你的结论DB=AD+CE.(不证明)
分析 (1)先判断出,∠BAD+∠CAE=90°,再判断出,∠ABD+∠BAD=90°,即可得到∠ABD=∠CAE,进而得出,△ABD≌△CAE即可得出结论;
(2)先判断出,∠BAD+∠CAE=90°,再判断出,∠ABD+∠BAD=90°,即可得到∠ABD=∠CAE,进而得出,△ABD≌△CAE即可得出结论;
(3)先用互余得出,∠BAD=∠AQD即可得出,△ABD∽△QAD,即:$\frac{DB}{AD}=\frac{AB}{AQ}$,再转化成$\frac{DB-AD}{AD}=\frac{CQ}{AQ}$,再判断出,△CEQ∽ADQ,即:$\frac{CE}{AD}=\frac{CQ}{AQ}$,即可得出结论.
解答 解:(1)DE=CE+BD,
理由:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥AP,
∴∠ABD+∠BAD=90°,
∴∠ABD=∠CAE,
∵CE⊥AP,BD⊥AP,
∴∠ADB=∠CEA=90°
在△ABD和△CAE中,$\left\{\begin{array}{l}{∠ADB=∠CEA}\\{∠ABD=∠CAE}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∴DE=AD+AE=CE+BD
(2)如图2,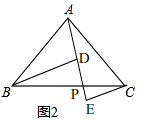
DE=BD-CE,
理由:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥AP,
∴∠ABD+∠BAD=90°,
∴∠ABD=∠CAE,
∵CE⊥AP,BD⊥AP,
∴∠ADB=∠CEA=90°
在△ABD和△CAE中,$\left\{\begin{array}{l}{∠ADB=∠CEA}\\{∠ABD=∠CAE}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CAE,
∴BD=AE,AD=CE,
∴DE=AE-AD=BD-CE,
故答案为:DE=BD-CE
(3)DB=AD+CE.
理由:∵∠BAC=90°,
∴∠BAD+∠QAD=90°,
∵AD⊥BQ,
∴∠QAD+∠AQD=90°,
∴∠BAD=∠AQD,
∵∠ADB=∠QDA,
∴△ABD∽△QAD,
∴$\frac{DB}{AD}=\frac{AB}{AQ}$,
∵AB=AC=AQ+CQ,
∴$\frac{DB}{AD}=\frac{AQ+CQ}{AQ}$,
∴$\frac{DB-AD}{AD}=\frac{CQ}{AQ}$
∵AD⊥BQ,CE⊥BQ,
∴∠ADQ=∠CEQ=90°,
∵∠AQD=∠CQE,
∴△CEQ∽ADQ,
∴$\frac{CE}{AD}=\frac{CQ}{AQ}$,
∴$\frac{DB-AD}{AD}=\frac{CE}{AD}$,
∴DB-AD=CE,
即:DB=AD+CE.
故答案为:DB=AD+CE.
点评 此题是三角形综合题,主要考查了同角的余角相等,全等三角形的判定和性质,相似三角形的判断和性质,比例的性质,解本题的关键是判断出,△ABD≌△CAE,难点是(3)中相似三角形的选用.是一道比较好的中考常考题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案①两个有理数相加,和一定大于每一个加数
②一个正数与一个负数相加得正数
③两个负数和的绝对值一定等于它们绝对值的和
④两个正数相加,和为正数
⑤正数加负数,其和一定等于0.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 32,42,52 | B. | 1.5,2,2.5 | C. | 6,8,10 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
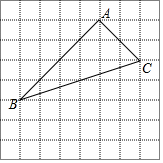 如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.
如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC. 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题: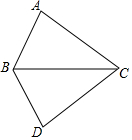 如图,∠ABC=∠DBC,请补充一个条件:AB=DB或∠A=∠D或∠ACB=∠DCB,使△ABC≌△DBC,并说明理由.
如图,∠ABC=∠DBC,请补充一个条件:AB=DB或∠A=∠D或∠ACB=∠DCB,使△ABC≌△DBC,并说明理由.