题目内容
11.已知(x+y)2=25,(x-y)2=1,求x2+y2与xy的值.分析 已知等式利用完全平方公式化简,相加减即可求出所求式子的值.
解答 解:∵(x+y)2=x2+2xy+y2=25①,(x-y)2=x2-2xy+y2=1②,
∴①+②得:2(x2+y2)=26,即x2+y2=13;
①-②得:4xy=24,即xy=6.
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
19.下列说法正确的是( )
| A. | 没有最大的正数,却有最大的负数 | B. | 数轴上离原点越远,表示数越大 | ||
| C. | 0大于一切负数 | D. | 在原点左边离原点越远,数就越大 |
16.一元二次方程3x2-5x=0的二次项系数和一次项系数分别是( )
| A. | 3,5 | B. | 3,-5 | C. | 3,0 | D. | 5,0 |
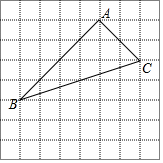 如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.
如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.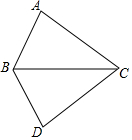 如图,∠ABC=∠DBC,请补充一个条件:AB=DB或∠A=∠D或∠ACB=∠DCB,使△ABC≌△DBC,并说明理由.
如图,∠ABC=∠DBC,请补充一个条件:AB=DB或∠A=∠D或∠ACB=∠DCB,使△ABC≌△DBC,并说明理由.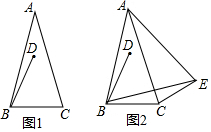 在△ABC中,AB=AC,∠BAC=α(0°<α<60°),BD=BC,∠DBC=60°.
在△ABC中,AB=AC,∠BAC=α(0°<α<60°),BD=BC,∠DBC=60°.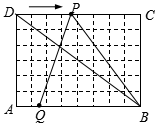 如图1,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.求运动时间t为多少秒时,△PQB成为以PQ为腰的等腰三角形?
如图1,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动.求运动时间t为多少秒时,△PQB成为以PQ为腰的等腰三角形?