题目内容

10．已知关于x的一元二次方程ax2+bx+c=3的一个根为x1=2，且抛物线y=ax2+bx+c的对称轴是直线x=2，则抛物线的顶点坐标为（2，3．

分析 利用方程解的定义得到x=2时，y=ax2+bx+c=3，即自变量为2时，函数值为3，然后根据二次函数的性质可确定抛物线的顶点坐标．

解答 解：∵关于x的一元二次方程ax2+bx+c=3的一个根为x1=2，
∴x=2时，y=ax2+bx+c=3，
而抛物线y=ax2+bx+c的对称轴是直线x=2，
∴抛物线的顶点坐标为（2，3）．
故答案为（2，3）．

点评 本题考查了抛物线与x轴的交点：对于二次函数y=ax2+bx+c（a，b，c是常数，a≠0），通过解方程ax2+bx+c=0可得到抛物线与x轴的交点的横坐标．也考查了二次函数的性质．

练习册系列答案
相关题目
20．在数轴上画出表示-1.5，-2，-3$\frac{1}{2}$，4及它们的相反数的点，并用“＜”号将所有的数连接起来．
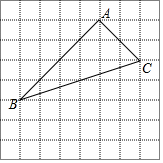1．如图，在边长为1的小正方形组成的方格纸中，有一个以格点为顶点的△ABC．
（1）试根据三角形三边关系，判断△ABC的形状；
（2）在方格纸中利用直尺分别画出AB、BC的垂直平分线（要求描出关键格点），交点为O．问点O到△ABC三个顶点的距离相等吗？说明理由．
18．若抛物线y=a（x-h）2+k上有点A（2，1），且当x=-2时，y有最大值3，则a=-$\frac{1}{8}$，h=-2，k=3．
5．计算：
（1）$\sqrt{18}$-$\sqrt{72}$+$\sqrt{50}$；
（2）（$\sqrt{7}$+$\sqrt{3}$）（$\sqrt{7}$-$\sqrt{3}$）-$\sqrt{16}$；
（3）$\frac{\sqrt{20}+\sqrt{5}}{\sqrt{45}}$-$\sqrt{\frac{1}{3}}$•$\sqrt{6}$；
（4）（2-$\sqrt{10}$）2+$\sqrt{40}$．
（5）（-2）3+$\frac{1}{2}$（2015-$\sqrt{3}$）0-|-$\frac{1}{2}$|；
（6）$\frac{2\sqrt{12}+\sqrt{3}}{\sqrt{3}}$+（1-$\sqrt{3}$）0．
15．化简：
（1）$\frac{{\sqrt{72}+\sqrt{32}}}{2}$-5；
（2）$\frac{{\sqrt{3}}}{2}$-3$\sqrt{\frac{1}{6}}$+2$\sqrt{216}$；
（3）（2$\sqrt{3}$+3$\sqrt{2}$）（2$\sqrt{3}$-3$\sqrt{2}$）；   
（4）$\sqrt{2}$（$\sqrt{18}$-2$\sqrt{3}$）+4$\sqrt{2}$×$\frac{{\sqrt{3}}}{2}$．
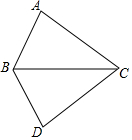2．如图，∠ABC=∠DBC，请补充一个条件：AB=DB或∠A=∠D或∠ACB=∠DCB，使△ABC≌△DBC，并说明理由．
19．下列说法正确的是（　　）
A．没有最大的正数，却有最大的负数B．数轴上离原点越远，表示数越大
C．0大于一切负数D．在原点左边离原点越远，数就越大
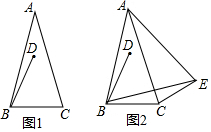20．在△ABC中，AB=AC，∠BAC=α（0°＜α＜60°），BD=BC，∠DBC=60°．
（1）如图1，直接写出∠ABD的度数（用含α的式子表示）；
（2）加图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并说明理由；
（3）在（2）的条件下，连接DE，若∠DEC=45°，求α的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网