��Ŀ����
11����֪���κ���y=ax2+bx+c�У��亯��y���Ա���x֮��IJ��ֶ�Ӧֵ�����ʾ��| x | �� | 0 | 1 | 2 | 3 | 4 | 5 | �� |
| y | �� | 4 | 1 | 0 | 1 | 4 | 9 | �� |
��2��������ͼ����x������ƽ��3����λ����д��ƽ�ƺ�ͼ������Ӧ�ĺ�����ϵʽ��y=��x-5��2��
��3�����P1��m��y1����P2��m+1��y2����P3��m+2��y3�����ڶ��κ���y=ax2+bx+c��ͼ���ϣ��ʣ���m��-3ʱ��y1��y2��y3��ֵһ������Ϊͬһ�����������ߵij���Ϊʲô��
���� ��1����x=1��3ʱ��y=1�����������ߵĶԳ��Կ�֪�������ߵĶԳ���Ϊx=2���ó���������Ϊ��2��0����
��2�����ݴ���ϵ������ý���ʽ��Ȼ�����ƽ�ƵĹ��ɼ�����ã�
��3���Ƚ���P1��P2��P3���������y=��x-2��2���õ�y1=��m-2��2��y2=��m-1��2��y3=m2���ٸ��ݲ���ʽ�����ʼ�m��-3�ó�y1��y2��y3��0��m+3��0��m-1��0��Ȼ���ж�y2+y3-y1��0����y2+y3��y1���������������߹�ϵ�������ɵó���m��-3ʱ��y1��y2��y3��ֵһ������Ϊͬһ�����������ߵij���
��� �⣺��1�����������ߵĶԳ��ԣ��۲�����֪��
�����ߵĶԳ���Ϊx=2����������Ϊ��2��0����
��2����������Ϊy=a��x-2��2��
���루1��1����ã�a=1��
��������Ϊy=��x-2��2��
�ɡ�����Ҽ�����ԭ���֪����������y=��x-2��2����ƽ��3����λ���õ������ߵı���ʽ��y=��x-2-3��2����y=��x-5��2��
��3����m��-3ʱ��y1��y2��y3��ֵһ������Ϊͬһ�����������ߵij����������£�
��y=��x-2��2��
��y1=��m-2��2��y2=��m-1��2��y3=m2��
��m��-3��
��y1��y2��y3��0��m+3��0��m-1��-4��0��
��y2+y3-y1=��m-1��2+m2-��m-2��2=m2+2m-3=��m+3����m-1����
��y2+y3-y1��0��
��y2+y3��y1��
�൱m��-3ʱ��y1��y2��y3��ֵһ������Ϊͬһ�����������ߵij���
�ʴ�Ϊ��2��0����y=��x-5��2��
���� ������Ҫ�����˶��κ���ͼ���ϵ�������������ô���ϵ��������κ����Ľ���ʽ�����κ��������ʣ�����ͼ���ƽ�ƹ��ɣ�����ʽ�����ʣ����������߹�ϵ������֪ʶ���ۺ��Խ�ǿ���Ѷ����У�

| A�� | 4.6��103Ԫ | B�� | 46��102Ԫ | C�� | 4.6��1011Ԫ | D�� | 0.46��1012Ԫ |
| A�� | ��-x+y����-x-y�� | B�� | ��a-2b����2b-a�� | C�� | ��a-b����a+b����a2+b2�� | D�� | ��a-b+c����a+b-c�� |
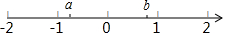 ʵ��a��b�������ϵ�λ����ͼ��ʾ������$\sqrt{��a+1��^{2}}$-$\sqrt{��b-1��^{2}}$-$\sqrt{��a-b��^{2}}$��
ʵ��a��b�������ϵ�λ����ͼ��ʾ������$\sqrt{��a+1��^{2}}$-$\sqrt{��b-1��^{2}}$-$\sqrt{��a-b��^{2}}$�� ��ͼ��ˮƽ���õ�Բ������ˮ�ܵ��Ľ���ֱ����1m����ˮ����ˮ��������CD��0.8m����ˮ���ABΪ0.8m��
��ͼ��ˮƽ���õ�Բ������ˮ�ܵ��Ľ���ֱ����1m����ˮ����ˮ��������CD��0.8m����ˮ���ABΪ0.8m��
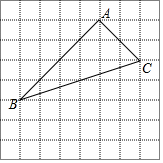 ��ͼ���ڱ߳�Ϊ1��С��������ɵķ���ֽ�У���һ���Ը��Ϊ����ġ�ABC��
��ͼ���ڱ߳�Ϊ1��С��������ɵķ���ֽ�У���һ���Ը��Ϊ����ġ�ABC��