题目内容
四边形ABCD中,∠B=∠D=90°,∠BAD和∠BCD的内(或外)角平分线分别为AE和CF.
(1)当AE,CF都为内角平分线时,不难证明AE∥CF.过程如下:(如图1)
∵∠BAD+∠BCD=∠1+∠2+∠3+∠4=360°-(∠B+∠D).而∠B=∠D=90°.∠1=∠2,3=∠4,
∴2(∠2+∠4)=360°-180°=180°
则∠2+∠4=90°
又∵∠B=90°∴,2+∠5=90°,则∠4=∠5.∴AE∥CF.
(2)当AE,CF时都为角平分线时(如图2),AE与CF位置关系怎样?给出证明.
(3)当AE是内角平分线,CF是外角平分线时(如图3),请你探索AE与CF的位置关系,并给出证明.

(1)当AE,CF都为内角平分线时,不难证明AE∥CF.过程如下:(如图1)
∵∠BAD+∠BCD=∠1+∠2+∠3+∠4=360°-(∠B+∠D).而∠B=∠D=90°.∠1=∠2,3=∠4,
∴2(∠2+∠4)=360°-180°=180°
则∠2+∠4=90°
又∵∠B=90°∴,2+∠5=90°,则∠4=∠5.∴AE∥CF.
(2)当AE,CF时都为角平分线时(如图2),AE与CF位置关系怎样?给出证明.
(3)当AE是内角平分线,CF是外角平分线时(如图3),请你探索AE与CF的位置关系,并给出证明.

考点:平行线的判定,垂线
专题:探究型
分析:(2)作DP∥AE,如图2,根据四边形内角和为360°得∠BAD+∠BCD=180°,则根据邻补角的定义得到∠GAD+∠BCH=180°,再根据角平分线先定义得∠1=
∠GAD,∠4=
∠BCH,所以∠1+∠4=90°,由PD∥AE得到∠1=∠2,而∠2+∠3=90°,则∠1+∠3=90°,理由等量代换得∠3=∠4,所以PD∥CF,于是得到AE∥CF;
(3)如图3,根据四边形内角和为360°得∠BAD+∠BCD=180°,则∠BAD=∠BCE,再由AE,CF时都为角平分线得∠1=
∠BAD,∠2=
∠BCE,则∠1=∠2,根据三角形内角和定理得∠5=∠B=90°,则AE⊥CF.
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图3,根据四边形内角和为360°得∠BAD+∠BCD=180°,则∠BAD=∠BCE,再由AE,CF时都为角平分线得∠1=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(2)AE∥CF.理由如下:
作DP∥AE,如图2,
∵四边形ABCD中,∠B=∠D=90°,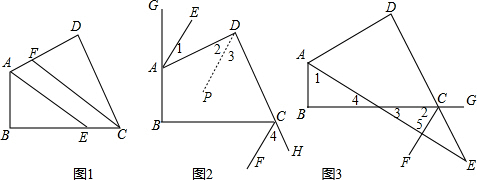
∴∠BAD+∠BCD=180°,
∴∠GAD+∠BCH=180°,
∵AE,CF时都为角平分线,
∴∠1=
∠GAD,∠4=
∠BCH,
∴∠1+∠4=90°,
∵PD∥AE,
∴∠1=∠2,
而∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠3=∠4,
∴PD∥CF,
∴AE∥CF;
(3)AE⊥CF.理由如下:
如图3,
∵四边形ABCD中,∠B=∠D=90°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠BCE,
∵AE,CF时都为角平分线,
∴∠1=
∠BAD,∠2=
∠BCE,
∴∠1=∠2,
而∠3=∠4,
∴∠5=∠B=90°,
∴AE⊥CF.
作DP∥AE,如图2,
∵四边形ABCD中,∠B=∠D=90°,

∴∠BAD+∠BCD=180°,
∴∠GAD+∠BCH=180°,
∵AE,CF时都为角平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠4=90°,
∵PD∥AE,
∴∠1=∠2,
而∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠3=∠4,
∴PD∥CF,
∴AE∥CF;
(3)AE⊥CF.理由如下:
如图3,
∵四边形ABCD中,∠B=∠D=90°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠BCE,
∵AE,CF时都为角平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2,
而∠3=∠4,
∴∠5=∠B=90°,
∴AE⊥CF.
点评:本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行.也考查了四边形的内角和和垂线.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

 已知:如图,AB∥CD,∠B=∠C.求证:∠E=∠F.(本题需要标注理由)
已知:如图,AB∥CD,∠B=∠C.求证:∠E=∠F.(本题需要标注理由)
 将一副三角板如图所示叠放,A、E、C、D在同一条直线上.
将一副三角板如图所示叠放,A、E、C、D在同一条直线上.