题目内容
3. 如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.
如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.
分析 设圆锥的底面圆的半径为r,由∠AOB=90°得到AB为圆形纸片的直径,则OB=$\frac{\sqrt{2}}{2}$AB=$\sqrt{2}$cm,根据弧长公式计算出扇形OAB的弧AB的长,然后根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长进行计算.
解答  解:设圆锥的底面圆的半径为r,
解:设圆锥的底面圆的半径为r,
连结AB,如图,
∵扇形OAB的圆心角为90°,
∴∠AOB=90°,
∴AB为圆形纸片的直径,
∴AB=2cm,
∴OB=$\frac{\sqrt{2}}{2}$AB=$\sqrt{2}$cm,
∴扇形OAB的弧AB的长=$\frac{90π×\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π,
∴2πr=$\frac{\sqrt{2}}{2}$π,
∴r=$\frac{\sqrt{2}}{4}$(cm).
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长.也考查了圆周角定理和弧长公式.

练习册系列答案
相关题目
13. 如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )
如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )
 如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )
如图,已知直线a∥b,∠1=40°,∠2=100°,则∠3等于( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
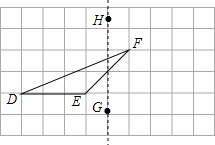 如图,在正方形网格上有一个△DEF.
如图,在正方形网格上有一个△DEF.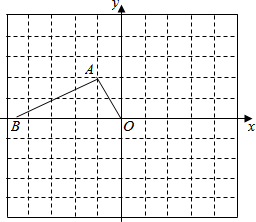 如图,在Rt△AOB中,∠A=90°,∠AOB=60°,在边长为1的小正方形组成的网格中,△AOB的顶点O、A均在格点上,点B在x轴上,点A的坐标为(-1,2).
如图,在Rt△AOB中,∠A=90°,∠AOB=60°,在边长为1的小正方形组成的网格中,△AOB的顶点O、A均在格点上,点B在x轴上,点A的坐标为(-1,2).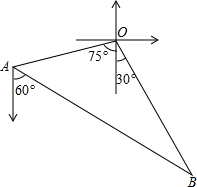 如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?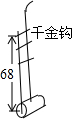 中国民间乐器二胡的“千斤钩”钩在弦长的黄金分割点处音质最好,一把二胡的弦长为68cm,求“千金钩”上、下两部分弦长.
中国民间乐器二胡的“千斤钩”钩在弦长的黄金分割点处音质最好,一把二胡的弦长为68cm,求“千金钩”上、下两部分弦长.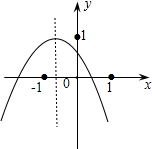 小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )
小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( ) 如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的度数为30度.
如图是一个风筝的图案,它是轴对称图形,量得∠B=30°,则∠E的度数为30度.