题目内容
18.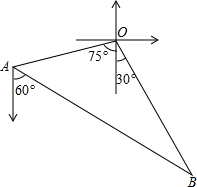 如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
分析 过O作OC⊥AB于C.先判断出△AOC是等腰直角三角形,判断出∠A和∠B的度数,利用三角函数求出BC的长,求出乙船从O点到B点所需时间为2小时,甲船追赶乙船速度为(15+15$\sqrt{3}$)海里/小时.
解答 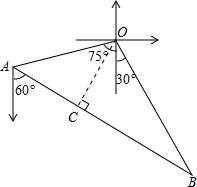 解:过O作OC⊥AB于C.
解:过O作OC⊥AB于C.
则∠OAC=180°-60°-75°=45°,
可知AO=15$\sqrt{2}$(海里),
∴OC=AC=15$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=15(海里),
∵∠B=90°-30°-30°=30°,
∴$\frac{OC}{BC}$=tan30°,
∴$\frac{15}{BC}$=$\frac{\sqrt{3}}{3}$,
∴BC=15$\sqrt{3}$(海里),
OB=15×2=30(海里),
乙船从O点到B点所需时间为2小时,
甲船追赶乙船速度为(15+15$\sqrt{3}$)海里/小时.
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
8.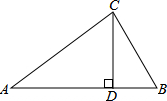 如图,CD是Rt△ABC斜边AB上的高,CD=6,BD=4,则AB的长为( )
如图,CD是Rt△ABC斜边AB上的高,CD=6,BD=4,则AB的长为( )
 如图,CD是Rt△ABC斜边AB上的高,CD=6,BD=4,则AB的长为( )
如图,CD是Rt△ABC斜边AB上的高,CD=6,BD=4,则AB的长为( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
6.在画二次函数的图象时列出了下表:
观察表格,可以得到许多信息:
(1)抛物线的对称轴是直线x=1;当x=-2时,对应的y值是-5;
(2)我们还发现,在对称轴右侧,当x每增加1个单位时,对应y值除了趋势逐渐变小外,在数量上还存在某种规律,试利用这一规律,直接写出当x=5时,对应的y值是-12;
(3)函数y=ax2+bx+c(a、b、c为常数,a≠0)图象上有三点:A(m,y1)、B(m+1,y2)、C(m+2,y3).通过计算说明:(y3-y2)与(y2-y1)的差为定值.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 0 | 3 | 4 | 3 | 0 | -5 | … |
(1)抛物线的对称轴是直线x=1;当x=-2时,对应的y值是-5;
(2)我们还发现,在对称轴右侧,当x每增加1个单位时,对应y值除了趋势逐渐变小外,在数量上还存在某种规律,试利用这一规律,直接写出当x=5时,对应的y值是-12;
(3)函数y=ax2+bx+c(a、b、c为常数,a≠0)图象上有三点:A(m,y1)、B(m+1,y2)、C(m+2,y3).通过计算说明:(y3-y2)与(y2-y1)的差为定值.
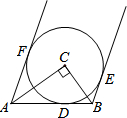 如图,在Rt△ABC中,∠C=90°,以点C为圆心作⊙C,与AB切于点D,过点A、B分别作⊙C的切线AF、BE,切点为F、E点.求证:AF∥BE.
如图,在Rt△ABC中,∠C=90°,以点C为圆心作⊙C,与AB切于点D,过点A、B分别作⊙C的切线AF、BE,切点为F、E点.求证:AF∥BE. 如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.
如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.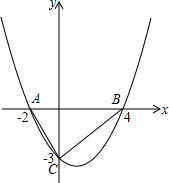 如图,二次函数的图象经过A、B、C三点
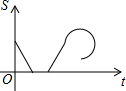
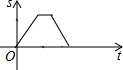
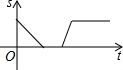
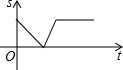
如图,二次函数的图象经过A、B、C三点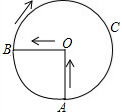 某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画出小江与中心O的距离S随时间t变化的图象是( )
某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画出小江与中心O的距离S随时间t变化的图象是( )