题目内容
13.解方程或解不等式:(1)$\sqrt{15}$x+$\sqrt{80}$=4x+5$\sqrt{3}$;
(2)$\sqrt{2}$(x-$\sqrt{3}$)≥$\sqrt{6}$(x+1).
分析 (1)根据二次根式的混合运算法则以及一元一次方程的解法求出即可;
(2)根据二次根式的混合运算法则结合一元一次不等式的解法解答即可.
解答 解:(1)$\sqrt{15}$x+$\sqrt{80}$=4x+5$\sqrt{3}$,
整理得:($\sqrt{15}$-4)x=5$\sqrt{3}$-4$\sqrt{5}$,
解得:x=$\frac{5\sqrt{3}-4\sqrt{5}}{\sqrt{15}-4}$=$\sqrt{5}$;
(2)$\sqrt{2}$(x-$\sqrt{3}$)≥$\sqrt{6}$(x+1)
整理得:x-$\sqrt{3}$≥$\sqrt{3}$(x+1),
(1-$\sqrt{3}$)x≥2$\sqrt{3}$
则x≤$\frac{2\sqrt{3}}{1-\sqrt{3}}$=-3-$\sqrt{3}$,
即x≤-3-$\sqrt{3}$.
点评 此题主要考查了二次根式的混合运算以及一元一次方程和一元一次不等式的解法,正确分母有理化是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.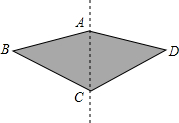 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
 如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.
如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.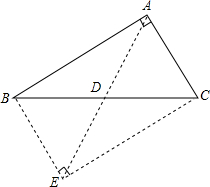 已知,如图所示,△ABC是直角三角形,∠BAC=90°,AD是BC边上的中线,求证:AD=BD=CD.
已知,如图所示,△ABC是直角三角形,∠BAC=90°,AD是BC边上的中线,求证:AD=BD=CD. 如图,A,B,C是同一直线上的三个点,图中共有几条射线?在不增加字母的情况下,能表示出的射线共几条?是哪几条?
如图,A,B,C是同一直线上的三个点,图中共有几条射线?在不增加字母的情况下,能表示出的射线共几条?是哪几条?