Question

13．如图，已知直线AB∥CD，过点A、C作直线l₁，过点B、D作直线l₂．

（1）如图1，点P在线段BD上（不与B、D重合）时，试写出∠APC、∠PAB、∠PCD之间的数量关系并说出理由；
（2）如图2，如果点P在BD的延长线上（不与D重合）时，（1）中的结论是否成立？若成立，请说明理由；若不成立，请你写出∠APC、∠PAB、∠PCD之间的数量关系并说出理由．
（3）如果点P在DB的延长线上（不与B重合）时，请在备用图上画出图形并直接写出∠APC、∠PAB、∠PCD之间的数量关系．

Answer 1

分析 （1）过P作PE∥AB，利用两直线平行，内错角相等即可解答；
（2）首先根据两直线平行得到∠BAP=∠AEC，再根据三角形的外角性质即可得到结论；
（3）首先根据两直线平行得到∠PEB=∠PCD，再根据三角形的外角性质即可得到结论．

解答 解：（1）如图1，过P作PE∥AB，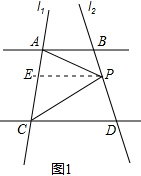
∵AB∥CD，
∴AB∥EP∥CD，
∴∠BAP=∠APE，∠PCD=∠CPE，
∴∠APC=∠PAB+∠PCD；



（2）如图2，设AP与CD交点为点E，
∵AB∥CD，
∴∠BAP=∠AEC，
∵∠AEC是△PCE的一个外角，
∴∠AEC=∠APC+∠PCD，
∴∠APC=∠PAB-∠PCD；





（3）如图3，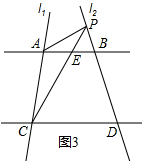
∵AB∥CD，
∴∠PEB=∠PCD，
∵∠PEB是△APE的一个外角，
∴∠PEB=∠PAB+∠APC，
∴∠APC=∠PCD-∠PAB．

点评 本题主要考查了平行线的性质以及三角形的外角性质，解题的关键是作图，构造平行线，利用平行线的性质以及三角形的外角知识进行解题，此题难度不大．