题目内容
 如图,经过点A(0,-4)的抛物线y=
如图,经过点A(0,-4)的抛物线y=| 1 |
| 2 |
(1)求抛物线的解析式并用配方法求顶点M的坐标;
(2)若抛物线上有一点P,使∠PCB=∠ABC,求P点坐标;
(3)将抛物线y=
| 1 |
| 2 |
| 7 |
| 2 |
考点:二次函数综合题,解一元一次不等式组,待定系数法求一次函数解析式,二次函数的性质,待定系数法求二次函数解析式
专题:综合题
分析:(1)只需运用待定系数法就可求出抛物线的解析式,然后用配方法就可求出顶点M的坐标;
(2)可分点P在x轴的下方和上方两种情况讨论,当点P在x轴下方时,根据抛物线的轴对称性得到点P的坐标;当点P在x轴上方时,直线PC与直线AB平行,可用待定系数法求出直线AB的解析式,然后再根据两平行直线一次项的系数相同,求出直线PC的解析式,然后只需求出直线PC与抛物线的交点坐标,就可解决问题;
(3)根据条件可得新抛物线的顶点M坐标为(1-m,-1),故点M始终在直线y=-1上.设直线y=-1与直线AB交于点P,与直线AC交于点Q,由点M在△ABC内可得点M在线段PQ上(不包括端点P、Q),只需求出点P、Q的坐标,就可解决问题.
(2)可分点P在x轴的下方和上方两种情况讨论,当点P在x轴下方时,根据抛物线的轴对称性得到点P的坐标;当点P在x轴上方时,直线PC与直线AB平行,可用待定系数法求出直线AB的解析式,然后再根据两平行直线一次项的系数相同,求出直线PC的解析式,然后只需求出直线PC与抛物线的交点坐标,就可解决问题;
(3)根据条件可得新抛物线的顶点M坐标为(1-m,-1),故点M始终在直线y=-1上.设直线y=-1与直线AB交于点P,与直线AC交于点Q,由点M在△ABC内可得点M在线段PQ上(不包括端点P、Q),只需求出点P、Q的坐标,就可解决问题.
解答:解:(1)∵点A(0,-4)、B(-2,0)在抛物线y=
x2+bx+c上,
∴
,
解得:
,
∴抛物线的解析式为y=
x2-x-4.
∵y=
x2-x-4=
(x2-2x+1-1)-4=
(x-1)2-
,
∴抛物线的顶点M的坐标为(1,-
);
(2)①点P在x轴的下方,如图1,

∵∠PCB=∠ABC,点B与点C关于对称轴x=1对称,
∴点A(0,-4)与点P也关于对称轴x=1对称,
∴点P的坐标为(2,-4);
②点P在x轴的上方,直线PC记为直线l,如图2,

令y=0,得
(x-1)2-
=0,
解得:x1=-2,x2=4,
∴点C的坐标为(4,0).
设直线AB的解析式为y=kx+t,
则有
,
解得:
,
∴直线AB的解析式为y=-2x-4.
∵∠PCB=∠ABC,
∴直线AB∥直线l,
∴直线l可设为y=-2x+n,
∵点C(4,0)在直线y=-2x+n上,
∴-8+n=0,
∴n=8,
∴直线l的解析式为y=-2x+8,
解方程组
,
得
或
,
∴点P的坐标为(-6,20).
综上所述:点P的坐标为(2,-4)或(-6,20);
(3)m的取值范围为-2<m<
.
解题过程如下:
由题可得新抛物线顶点M的坐标为(1-m,-
+
)即(1-m,-1).
设直线AC的解析式为y=px+q,
则有
,
解得:
,
∴直线AC的解析式为y=x-4.
设直线y=-1与直线AB交于点P,与直线AC交于点Q,如图3,

由-2x-4=-1,得x=-
,则点P的坐标为(-
,-1);
由x-4=-1,得x=3,则点P的坐标为(3,-1).
∵新抛物线的顶点M(1-m,-1)在△ABC内,
∴点M在线段PQ上(不包括端点P、Q),
∴
,
解得:-2<m<
.
| 1 |
| 2 |
∴
|
解得:
|
∴抛物线的解析式为y=
| 1 |
| 2 |
∵y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴抛物线的顶点M的坐标为(1,-
| 9 |
| 2 |
(2)①点P在x轴的下方,如图1,

∵∠PCB=∠ABC,点B与点C关于对称轴x=1对称,
∴点A(0,-4)与点P也关于对称轴x=1对称,
∴点P的坐标为(2,-4);
②点P在x轴的上方,直线PC记为直线l,如图2,

令y=0,得
| 1 |
| 2 |
| 9 |
| 2 |
解得:x1=-2,x2=4,
∴点C的坐标为(4,0).
设直线AB的解析式为y=kx+t,
则有
|
解得:
|
∴直线AB的解析式为y=-2x-4.
∵∠PCB=∠ABC,
∴直线AB∥直线l,
∴直线l可设为y=-2x+n,
∵点C(4,0)在直线y=-2x+n上,
∴-8+n=0,
∴n=8,
∴直线l的解析式为y=-2x+8,
解方程组
|
得
|
|
∴点P的坐标为(-6,20).
综上所述:点P的坐标为(2,-4)或(-6,20);
(3)m的取值范围为-2<m<
| 5 |
| 2 |
解题过程如下:
由题可得新抛物线顶点M的坐标为(1-m,-
| 9 |
| 2 |
| 7 |
| 2 |
设直线AC的解析式为y=px+q,
则有
|
解得:
|
∴直线AC的解析式为y=x-4.
设直线y=-1与直线AB交于点P,与直线AC交于点Q,如图3,

由-2x-4=-1,得x=-
| 3 |
| 2 |
| 3 |
| 2 |
由x-4=-1,得x=3,则点P的坐标为(3,-1).
∵新抛物线的顶点M(1-m,-1)在△ABC内,
∴点M在线段PQ上(不包括端点P、Q),
∴
|
解得:-2<m<
| 5 |
| 2 |
点评:本题主要考查了用待定系数法求抛物线及直线的解析式、抛物线的轴对称性、解不等式组等知识,正确进行分类是解决第(2)小题的关键,考虑临界位置是解决第(3)小题的关键.

练习册系列答案
相关题目
 在如图的直角坐标系中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点),点A的坐标为(-2,3).
在如图的直角坐标系中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点),点A的坐标为(-2,3).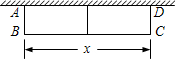 如图,一边利用墙,其余各边用篱笆靠墙围成矩形花圈ABCD,在花圈中间用一道篱笆隔成两个小矩形,墙可利用的最大长度为15m,篱笆总长为24m,设平行于墙的BC边长c m,矩形ABCD的面积为S m2.
如图,一边利用墙,其余各边用篱笆靠墙围成矩形花圈ABCD,在花圈中间用一道篱笆隔成两个小矩形,墙可利用的最大长度为15m,篱笆总长为24m,设平行于墙的BC边长c m,矩形ABCD的面积为S m2.