题目内容
7.(1)解方程组:$\left\{\begin{array}{l}{5x+2y=25,…①}\\{3x+4y=15;…②}\end{array}\right.$(2)解不等式组$\left\{\begin{array}{l}{x+1>0,…①}\\{x≤\frac{x-2}{3}+2,…②}\end{array}\right.$并写出这个不等式组的最大整数解.
分析 (1)根据方程组的解法计算即可;
(2)此题可先根据一元一次不等式组解出x的取值,根据x是最大整数解得出.
解答 解:(1)①×2得:10x+4y=50③,
③-②,得:7x=35,
解得:x=5,
把x=5代入①得:y=0,
所以方程组的解为:$\left\{\begin{array}{l}{x=5}\\{y=0}\end{array}\right.$;
(2)由①,得:x>-1,
由②,得:x≤2,
所以不等式组的解集为:-1<x≤2,
所以不等式组的最大整数解是2.
点评 本题考查了不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
18.分式方程$\frac{2}{x-3}=\frac{3}{x}$的解是( )
| A. | x=-9 | B. | x=9 | C. | x=3 | D. | $x=\frac{9}{5}$ |
2.如果a<b,那么下列不等式中正确的是( )
| A. | a-3>b-3 | B. | -3+a>-3+b | C. | 3a>3b | D. | -3a>-3b |
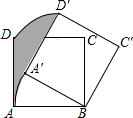 如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.
如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.