题目内容
16.(1)计算:(-$\frac{1}{2}$)-1-(3.14-π)0-tan60°+$\sqrt{12}$;(2)先化简$\frac{{x}^{2}-2x+1}{x+1}$÷$\frac{x-1}{{x}^{2}+x}$+x,然后再选择一个合适的x的值代入求值.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先算除法,再算加减,最后选取合适的x的值代入进行计算即可.
解答 解:(1)原式=-2-1-$\sqrt{3}$+2$\sqrt{3}$
=-3+$\sqrt{3}$;
(2)原式=$\frac{(x-1)^{2}}{x+1}$•$\frac{x(x+1)}{x-1}$+x
=x(x-1)+x
=x2-x+x
=x2,
当x=2时,原式=4.
点评 本题考查的是分式的化简求值,在解答此类题目时要注意分式要化为最简形式,再代入求值.

练习册系列答案
相关题目
4.下列各式中,属于二元一次方程的是( )
| A. | x2+y=0 | B. | $\frac{x+y}{3}$-2y=1 | C. | x=$\frac{2}{y}$+1 | D. | y+$\frac{1}{2}$x |
5.下列不等式中,不含有x=-1这个解的是( )
| A. | 2x+1≤-3 | B. | 2x-1≥-3 | C. | -2x+1≥3 | D. | -2x-1≤3 |
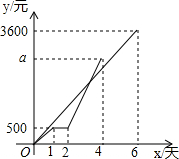 甲、乙两专卖店某段时间内销售收入y(元)与天数x(天)的函数图象如图,在这期间乙专卖店因故停业一天,重新开业后,乙专卖店的日均销售收入是原来的2倍,请解决下列问题:
甲、乙两专卖店某段时间内销售收入y(元)与天数x(天)的函数图象如图,在这期间乙专卖店因故停业一天,重新开业后,乙专卖店的日均销售收入是原来的2倍,请解决下列问题: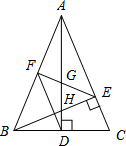 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确的有( )
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确的有( )