题目内容
12．解方程：（1）x2+4x=5；
（2）（2x-1）2-x2=0．
分析 （1）移项后分解因式，即可得出两个一元一次方程，求出方程的解即可；
（2）先分解因式，即可得出两个一元一次方程，求出方程的解即可．
解答 解：（1）x2+4x=5，
x2+4x-5=0，
（x+5）（x-1）=0，
x+5=0，x-1=0，
x1=-5，x2=1；
（2）（2x-1）2-x2=0，
（2x-1+x）（2x-1-x）=0，
2x-1+x=0，2x-1-x=0，
x1=$\frac{1}{3}$，x2=1．
点评 本题考查了解一元二次方程的应用，能把一元二次方程转化成一元一次方程是解此题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
2．
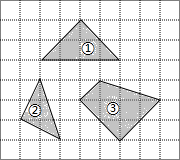如图，在正方形网格中，每个小正方形的边长均相等．网格中三个多边形（分别标记为①，②，③）的顶点均在格点上．被一个多边形覆盖的网格线中，竖直部分线段长度之和记为m，水平部分线段长度之和记为n，则这三个多边形中满足m=n的是（ ）
如图，在正方形网格中，每个小正方形的边长均相等．网格中三个多边形（分别标记为①，②，③）的顶点均在格点上．被一个多边形覆盖的网格线中，竖直部分线段长度之和记为m，水平部分线段长度之和记为n，则这三个多边形中满足m=n的是（ ）| A． | 只有② | B． | 只有③ | C． | ②③ | D． | ①②③ |
17．根据如表回答下列问题：
（1）268.96的平方根是±16.4．
（2）$\sqrt{28561}$≈169．
（3）$\sqrt{273}$在那两个相邻数之间？为什么？
| x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
| x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
（2）$\sqrt{28561}$≈169．
（3）$\sqrt{273}$在那两个相邻数之间？为什么？
4．下列各式中，属于二元一次方程的是（ ）
| A． | x2+y=0 | B． | $\frac{x+y}{3}$-2y=1 | C． | x=$\frac{2}{y}$+1 | D． | y+$\frac{1}{2}$x |