题目内容
17.解不等式组,并把解集用数轴表示出来.$\left\{\begin{array}{l}{-3(x+1)-(x-3)<8}\\{\frac{2x+1}{3}-\frac{1-x}{2}≤1}\end{array}\right.$.
分析 分别求出各不等式的解集,再求出其公共解集并在数轴上表示出来即可.
解答 解:$\left\{\begin{array}{l}{-3(x+1)-(x-3)<8①}\\{\frac{2x+1}{3}-\frac{1-x}{2}≤1②}\end{array}\right.$,
解不等式①得,x>-2,
解不等式②得,x≤1,
故不等式组的解集为:-2<x≤1,
在数轴上表示为:
点评 本题考查的是解一元一次不等式组及在数轴上表示不等式组的解集,熟知实心圆点与空心圆圈的区别是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.为解方程x4-5x2+4=0,我们可设x2=y,则x4=y2,原方程可化为y2-5y+4=0.解得y1=1,y2=4,当y=1时,x2=1,所以x=±1;当y=4时,x2=4,所以x=±2.故原方程的解为x1=1,x2=-1,x3=2,x4=-2.以上解题方法主要体现的数学思想是( )
| A. | 数形结合 | B. | 换元与降次 | C. | 消元 | D. | 公理化 |
12.不等式组$\left\{\begin{array}{l}{x-1>0}\\{2x<4}\end{array}\right.$的解是( )
| A. | x>1 | B. | x<2 | C. | 1<x<2 | D. | 无解 |
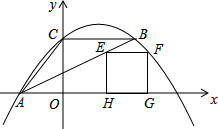 如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO,二次函数y=ax2-5ax+4的图象经过△ABC的三个顶点.
如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO,二次函数y=ax2-5ax+4的图象经过△ABC的三个顶点.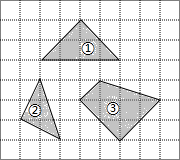 如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是( )
如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是( )