题目内容
8.解不等式(组),并将解集表示在数轴上:(1)$\frac{2x-1}{3}$-4<-$\frac{x+4}{2}$
(2)x-(3x-1)≤x+2
(3)$\left\{\begin{array}{l}5x-2>3(x+1)\\ \frac{1}{2}x-1≥7-\frac{3}{2}x\end{array}\right.$
(4)$\left\{\begin{array}{l}\frac{1}{2}x+1<2(x-1)\\ \frac{x}{3}>\frac{x+2}{5}\end{array}\right.$.
分析 (1)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得;
(2)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;
(3)分别求出每一个不等式的解集,根据口诀“同大取大”即可确定不等式组的解集;
(4)分别求出每一个不等式的解集,根据口诀“同大取大”即可确定不等式组的解集.
解答 解:(1)去分母,得:2(2x-1)-24<-3(x+4),
去括号,得:4x-2-24<-3x-12,
移项,得:4x+3x<-12+2+24,
合并同类项,得:7x<14,
系数化为1,得:x<2,
将不等式的解集表示在数轴上如下: ;
;
(2)去括号,得:x-3x+1≤x+2,
移项,得:x-3x-x≤2-1,
合并同类项,得:-3x≤1,
系数化为1,得:x≥-$\frac{1}{3}$,
将不等式的解集表示在数轴上如下: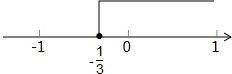 ;
;
(3)解不等式5x-2≥3(x+1),得:x≥$\frac{5}{2}$,
解不等式$\frac{1}{2}$x-1≥7-$\frac{3}{2}$x,得:x≥4,
∴不等式组的解集为x≥4,
将不等式的解集表示在数轴上如下: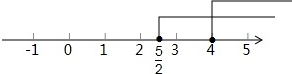 ;
;
(4)解不等式$\frac{1}{2}$x+1<2(x-1),得:x>2,
解不等式$\frac{x}{3}$>$\frac{x+2}{5}$,得:x>3,
∴不等式组的解集为:x>3,
将不等式的解集表示在数轴上如下: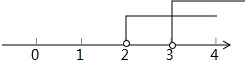 ;
;
点评 本题考查的是解一元一次不等式和解一元一次不等式组的能力,熟练掌握不等式的基本性质以准确求出每个不等式的解集是解答此题的关键.

练习册系列答案
相关题目
11.下列运算正确的是( )
| A. | x4+x4=x8 | B. | x2•x=x3 | C. | (x2)3=x5 | D. | x6÷x2=x3 |
16.顺次连结菱形四边中点所得的四边形一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 等腰梯形 |
20. 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )| A. | (3,4)或(2,4) | B. | (2,4)或(8,4) | C. | (3,4)或(8,4) | D. | (3,4)或(2,4)或(8,4) |
17.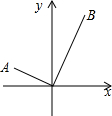 如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
 如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )| A. | 2$\sqrt{5}$ | B. | 4 | C. | $\sqrt{5}$ | D. | 2 |
18.等腰△ABC中,已知有一条边长为4,另一条边长为9,则△ABC的周长为( )
| A. | 13 | B. | 17 | C. | 22 | D. | 17或22 |
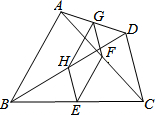 如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB、CD应满足的条件是AB=CD.
如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB、CD应满足的条件是AB=CD. 如图,在菱形ABCD中,E是AB的中点,F是AC的中点,如果EF=4,那么CD=8.
如图,在菱形ABCD中,E是AB的中点,F是AC的中点,如果EF=4,那么CD=8.