题目内容
19．
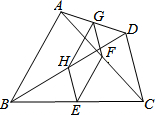如图，在四边形ABCD中，E，F，G，H分别是BC，AC，AD，BD的中点，要使四边形EFGH是菱形，四边形ABCD的边AB、CD应满足的条件是AB=CD．
分析 利用三角形中位线定理可以证得四边形EFGH是平行四边形，然后由菱形的判定定理进行解答．
解答 解：要使四边形EFGH是菱形，四边形ABCD的边AB、CD应满足的条件是：AB=CD，
理由：∵在四边形ABCD中，E、F、G、H分别是BC，AC，AD，BD的中点，
∴EF∥AB，HG∥AB，
∴EF∥HG；
同理，HE∥GF，
∴四边形EFGH是平行四边形，
∵AB=CD，
∴GH=GF，
所以平行四边形EFGH是菱形．
故答案为：AB=CD．
点评 本题考查了中点四边形、菱形的判定与性质．菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：①定义；②四边相等；③对角线互相垂直平分．
练习册系列答案
阅读快车系列答案
相关题目
2．
如图，在矩形ABCD中，点E在AD上，且EC平分∠BED，AB=1，∠ABE=45°，则BC的长为（ ）
如图，在矩形ABCD中，点E在AD上，且EC平分∠BED，AB=1，∠ABE=45°，则BC的长为（ ）| A． | $\sqrt{2}$ | B． | 1.5 | C． | $\sqrt{3}$ | D． | 2 |
已知：如图，AB∥DC，AC和BD相交于点O，E是CD上一点，F是OD上一点，且∠1=∠A．
7．对角线互相垂直平分且相等的四边形一定是（ ）
| A． | 正方形 | B． | 菱形 | C． | 矩形 | D． | 平行四边形 |
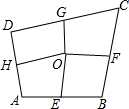如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若S四边形AEOH=4，S四边形BFOE=5，S四边形CGOF=6，则S四边形DHOG=5．
如图，AB交CD于O，OE⊥AB．
如图，在Rt△ABC中，∠BAC=90°，∠ABC的平分线BD交AC于点D，DE是BC的垂直平分线，点E是垂足．已知AD=2，则图中长为2$\sqrt{3}$的线段有（ ）