题目内容
17.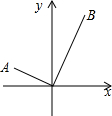 如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )
如图,在平面直角坐标系中有A,B两点,其中点A的坐标是(-2,1),点B的横坐标是2,连接AO,BO.已知∠AOB=90°,则点B的纵坐标是( )| A. | 2$\sqrt{5}$ | B. | 4 | C. | $\sqrt{5}$ | D. | 2 |
分析 先过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,构造相似三角形,再利用相似三角形的性质列出比例式,计算求解即可.
解答 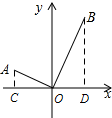 解:过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,则∠ACO=∠ODB=90°,∠B+∠BOD=90°,
解:过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,则∠ACO=∠ODB=90°,∠B+∠BOD=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠B=∠AOC,
∴△ACO∽△ODB,
∴$\frac{AC}{OD}=\frac{CO}{DB}$,
又∵A的坐标是(-2,1),点B的横坐标是2,
∴$\frac{1}{2}=\frac{2}{DB}$,即DB=4,
∴点B的纵坐标是4.
故选(B).
点评 本题主要考查了相似三角形的判定与性质,通过作垂线构造相似三角形是解决问题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
7.对角线互相垂直平分且相等的四边形一定是( )
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
9. 如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知AD=2,则图中长为2$\sqrt{3}$的线段有( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知AD=2,则图中长为2$\sqrt{3}$的线段有( )
 如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知AD=2,则图中长为2$\sqrt{3}$的线段有( )
如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知AD=2,则图中长为2$\sqrt{3}$的线段有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
7.下列各式从左到右的变形是因式分解的是( )
| A. | m(a+b)=ma+mb | B. | a2-a=2=a(a-1)-2 | ||
| C. | -4a2+9b2=(-2a+3b)(2a+3b) | D. | x2-$\frac{1}{{y}^{2}}$=(x-$\frac{1}{y}$)(x+$\frac{1}{y}$) |

 如图,请写出能判定AD∥BC的一个条件∠2=∠B或∠1=∠C.
如图,请写出能判定AD∥BC的一个条件∠2=∠B或∠1=∠C. 已知:如图,△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且CF=DE,求证:∠CDF=∠A.
已知:如图,△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且CF=DE,求证:∠CDF=∠A.