题目内容
3．若菱形的两条对角线长分别为10cm和24cm，则顺次连接这个菱形四条边的中点所得的四边形的面积是60cm2．分析 先根据中点可知：HG是△BDC的中位线，得平行相似，则S△CHG=$\frac{1}{4}$S△DBC，同理得S△AEF=$\frac{1}{4}$S△BAD，
S△DEH=$\frac{1}{4}$S△ADC，S△BFG=$\frac{1}{4}$S△BAC，则S△CHG+S△AEF+S△DEH+S△BFG=$\frac{1}{2}$S四边形ABCD，代入计算即可．
解答 解：菱形ABCD中，E、F、G、H分别是AD、AB、BC、CD的中点，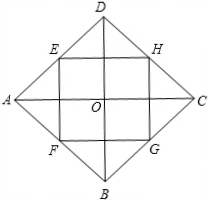
∴HG是△BDC的中位线，
∴HG∥BD，
∴△CHG∽△CDB，
∴S△CHG=$\frac{1}{4}$S△DBC，
同理S△AEF=$\frac{1}{4}$S△BAD，
∴S△CHG+S△AEF=$\frac{1}{4}$S△DBC+$\frac{1}{4}$S△BAD=$\frac{1}{4}$S四边形ABCD，
同理S△DEH+S△BFG=$\frac{1}{4}$S四边形ABCD，
∴S△CHG+S△AEF+S△DEH+S△BFG，
=$\frac{1}{4}$S四边形ABCD+$\frac{1}{4}$S四边形ABCD，
=$\frac{1}{2}$S四边形ABCD，
∴S中点四边形EFGH=$\frac{1}{2}$S四边形ABCD=$\frac{1}{2}$×$\frac{1}{2}$×10×24=60；
故答案为：120．
点评 本题考查了中点四边形和菱形的性质，运用三角形中位线的性质：三角形的中位线平行于第三边，且等于第三边的一半；可知平行相似且面积比是相似比的平方，从而得出中点四边形的面积是菱形面积的一半．
练习册系列答案
相关题目
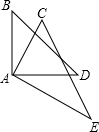将一副三角板如图摆放，若∠BAC=31°45′，则∠EAD的度数是31°45′．
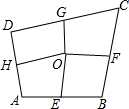如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若S四边形AEOH=4，S四边形BFOE=5，S四边形CGOF=6，则S四边形DHOG=5．
15．
如图，直线AB与直线CD相交于点O，MO⊥AB，垂足为O，已知∠AOD=136°，则∠COM的度数为（ ）
如图，直线AB与直线CD相交于点O，MO⊥AB，垂足为O，已知∠AOD=136°，则∠COM的度数为（ ）| A． | 36° | B． | 44° | C． | 46° | D． | 54° |