Question

20．已知：如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，则P点的坐标为（　　）

• A． （3，4）或（2，4）
• B． （2，4）或（8，4）
• C． （3，4）或（8，4）
• D． （3，4）或（2，4）或（8，4）

Answer 1

分析 此题分二种情况（1）OD是等腰三角形的底边时，（2）OD是等腰三角形的一条腰时，①若点O是顶角顶点时，②若D是顶角顶点时，分别进行讨论得出P点的坐标，再选择即可．

解答 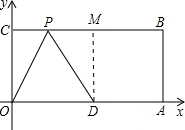解：（1）OD是等腰三角形的底边时，P就是OD的垂直平分线与CB的交点，此时OP=PD≠5；
（2）OD是等腰三角形的一条腰时：
①若点O是顶角顶点时，P点就是以点O为圆心，以5为半径的弧与CB的交点，
在直角△OPC中，CP=$\sqrt{O{P}^{2}-C{O}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3，
则P的坐标是（3，4）．
②若D是顶角顶点时，P点就是以点D为圆心，以5为半径的弧与CB的交点，
过D作DM⊥BC于点M，
在直角△PDM中，PM=$\sqrt{P{D}^{2}-D{M}^{2}}$=3，
当P在M的左边时，CP=5-3=2，则P的坐标是（2，4）；
当P在M的右侧时，CP=5+3=8，则P的坐标是（8，4）．
故P的坐标为：（3，4）或（2，4）或（8，4）．
故选D．

点评 此题主要考查了矩形的性质以及坐标与图形的性质和等腰三角形的性质，根据△ODP是腰长为5的等腰三角形进行分类讨论是解决问题的关键．