题目内容
(1)求比例式4:3=5:x中x的值.
(2)计算:cos245°+tan60°•sin60°.
(2)计算:cos245°+tan60°•sin60°.
考点:比例的性质,特殊角的三角函数值
专题:
分析:(1)根据比例的性质,可得x的值;
(2)根据特殊角三角函数值,可得实数,根据实数的运算,可得答案.
(2)根据特殊角三角函数值,可得实数,根据实数的运算,可得答案.
解答:解:(1)由比例的性质,得4x=3×5,
解得x=
;
(2)原式=(
)2+
×
=
+
=2.
解得x=
| 15 |
| 4 |
(2)原式=(
| ||
| 2 |
| 3 |
| ||
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
=2.
点评:本题考查了比例的性质,(1)利用了比例的性质,(2)要熟记特殊角三角函数值.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 如图,不能判定EB∥AC的条件是( )
如图,不能判定EB∥AC的条件是( )| A、∠C=∠DBE |
| B、∠A=∠ABE |
| C、∠C+∠EBC=180° |
| D、∠C=∠ABC |
已知a2+b2=5且ab=2,求式子a+b的值是( )
| A、3 | B、4 | C、±3 | D、±4 |
我市某一周每天的最高气温统计如下:17,18,19,19,20,19,18(单位:℃),则这组数据的极差与众数分别是( )
| A、2、18 | B、2、19 |
| C、3、18 | D、3、19 |
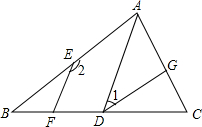 如图,AD∥EF,∠1+∠2=180°,
如图,AD∥EF,∠1+∠2=180°, 如图,AB∥CD,直线EF与AB,CD分别交于点G,H,GM平分∠BGH交CD于点M,∠1=50°,则∠2=
如图,AB∥CD,直线EF与AB,CD分别交于点G,H,GM平分∠BGH交CD于点M,∠1=50°,则∠2=