题目内容
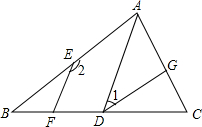 如图,AD∥EF,∠1+∠2=180°,
如图,AD∥EF,∠1+∠2=180°,(1)求证:DG∥AB.在下列橫线上填写:
证明:∵AD∥EF(已知)
∴
又∵∠1+∠2=180°(已知),
∴
∴DG∥AB (
(2)若DG是∠ADC的角平分线,∠1=30°,求∠B的度数.
考点:平行线的判定与性质
专题:推理填空题
分析:(1)根据平行线的性质定理以及判定定理即可解答;
(2)根据角平分线的定义以及平行线的性质定理即可求解.
(2)根据角平分线的定义以及平行线的性质定理即可求解.
解答:解:(1)证明:∵AD∥EF(已知)
∴∠2+∠BAD=180°(两直线平行,同旁内角互补)
又∵∠1+∠2=180°(已知),
∴∠1=∠BAD(同角的补角相等)
∴DG∥AB (内错角相等,两直线平行);
(2)证明:∵DG是∠ADC的角平分线,
∴∠GDC=∠1=30°,
又∵DG∥AB,
∴∠B=∠GDC=30°.
∴∠2+∠BAD=180°(两直线平行,同旁内角互补)
又∵∠1+∠2=180°(已知),
∴∠1=∠BAD(同角的补角相等)
∴DG∥AB (内错角相等,两直线平行);
(2)证明:∵DG是∠ADC的角平分线,
∴∠GDC=∠1=30°,
又∵DG∥AB,
∴∠B=∠GDC=30°.
点评:本题考查了平行线的性质定理和判定定理,理解定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有理数a、b在数轴上的位置如图所示,则下列各式中错误的是( )
有理数a、b在数轴上的位置如图所示,则下列各式中错误的是( )| A、b<0<a |
| B、|b|>|a| |
| C、a+b>0 |
| D、ab<0 |
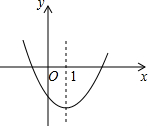 二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
二次函数y=ax2+bx+c图象如图,下列正确的个数为( )①abc>0;②2a-3c<0;③2a+b>0;④ax2+bx+c=0有两个实数解x1,x2,且x1+x2<0; ⑤9a+3b+c>0;⑥当x<1时,y随x增大而减小.
| A、2 | B、3 | C、4 | D、5 |
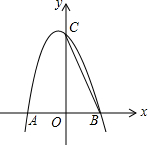 已知抛物线y=x2-2x+3经过B(1,0)、C(0,3),将直线BC向下平移,与抛物线交于点B′、C′(B′与B对应,C′与C对应),与y轴交于点D,当点D是线段B′C′的三等分点时,求点D的坐标.
已知抛物线y=x2-2x+3经过B(1,0)、C(0,3),将直线BC向下平移,与抛物线交于点B′、C′(B′与B对应,C′与C对应),与y轴交于点D,当点D是线段B′C′的三等分点时,求点D的坐标. 已知有理数a,b在数轴上表示的点如图所示,则下列式子中不正确的是( )
已知有理数a,b在数轴上表示的点如图所示,则下列式子中不正确的是( )| A、a•b<0 |
| B、a+b<0 |
| C、|a|<|b| |
| D、b-a>0 |
已知sinα<0.5,那么锐角α的取值范围是( )
| A、60°<α<90° |
| B、30°<α<90° |
| C、0°<α<60° |
| D、0°<α<30° |
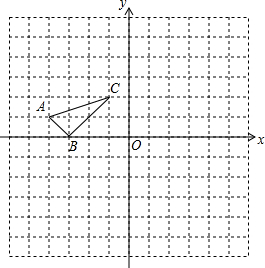 每个小正方形边长都为1个单位长度.
每个小正方形边长都为1个单位长度. 如图,梯形ABCD沿上底AD方向向右平移到梯形EFGH,AD=4,BC=8,若阴影部分面积是四边形ABGH的
如图,梯形ABCD沿上底AD方向向右平移到梯形EFGH,AD=4,BC=8,若阴影部分面积是四边形ABGH的