题目内容
如图，不能判定EB∥AC的条件是（ ）| A、∠C=∠DBE |
| B、∠A=∠ABE |
| C、∠C+∠EBC=180° |
| D、∠C=∠ABC |
考点：平行线的判定
专题：
分析：根据同位角相等、内错角相等、同旁内角互补，两直线平行即可判断．
解答：解：A．∠C=∠DBE，由同位角相等，两直线平行，可判断EB∥AC；
B．∠A=∠ABE，由内错角相等，两直线平行，可判断EB∥AC；
C．∠C+∠EBC=180°，由同旁内角互补，两直线平行，可判断EB∥AC；
D．∠C=∠ABC，不能判断EB∥AC．
故选：D．
B．∠A=∠ABE，由内错角相等，两直线平行，可判断EB∥AC；
C．∠C+∠EBC=180°，由同旁内角互补，两直线平行，可判断EB∥AC；
D．∠C=∠ABC，不能判断EB∥AC．
故选：D．
点评：此题考查了平行线的判定，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
练习册系列答案
相关题目
有理数a、b在数轴上的位置如图所示，则下列各式中错误的是（ ）| A、b＜0＜a |
| B、|b|＞|a| |
| C、a+b＞0 |
| D、ab＜0 |
已知有理数a，b在数轴上表示的点如图所示，则下列式子中不正确的是（ ）| A、a•b＜0 |
| B、a+b＜0 |
| C、|a|＜|b| |
| D、b-a＞0 |
已知sinα＜0.5，那么锐角α的取值范围是（ ）
| A、60°＜α＜90° |
| B、30°＜α＜90° |
| C、0°＜α＜60° |
| D、0°＜α＜30° |
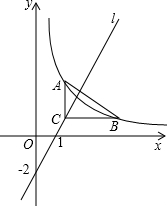已知直线l经过点（1，0）（0，-2），Rt△ABC如图放置，其直角顶点C在直线l上，两直角边分别平行于坐标轴，AC=2，BC=3，将Rt△ABC沿直线l平移，使点A、B都在函数y=