题目内容
用因式分解中的待定系数法解:已知多项式x2+axy+by2-5x+y+6的一个因式为x+y-2,求a+b的值.
考点:因式分解的应用
专题:
分析:将原式化为一因式与(x+y-2)积的形式,然后得到对应系数相等即可求得a、b的值.
解答:解:设x2+axy+by2-5x+y+6=(x+y-2)(cx+dy+m)=cx2+(c+d)xy+dy2+(m-2c)x+(m-2d)y-2m (实际上就是右边展开后的各项要和左边的一样)
则c=1,d=b,-2m=6,
所以 m=-3
所以x2+axy+by2-5x+y+6=(x+y-2)(x+by-3)=x2+(b+1)xy+by2-5x+(-3-2b)y+6
所以-3-2b=1,则b=-2
所以 a=b+1=-1
则a+b=-3.
则c=1,d=b,-2m=6,
所以 m=-3
所以x2+axy+by2-5x+y+6=(x+y-2)(x+by-3)=x2+(b+1)xy+by2-5x+(-3-2b)y+6
所以-3-2b=1,则b=-2
所以 a=b+1=-1
则a+b=-3.
点评:本题考查了因式分解的应用.利用因式分解最后整理成多项式的乘积等于0的形式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
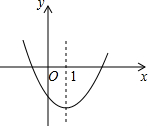 二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
二次函数y=ax2+bx+c图象如图,下列正确的个数为( )①abc>0;②2a-3c<0;③2a+b>0;④ax2+bx+c=0有两个实数解x1,x2,且x1+x2<0; ⑤9a+3b+c>0;⑥当x<1时,y随x增大而减小.
| A、2 | B、3 | C、4 | D、5 |
已知sinα<0.5,那么锐角α的取值范围是( )
| A、60°<α<90° |
| B、30°<α<90° |
| C、0°<α<60° |
| D、0°<α<30° |
下列事件中,属于必然事件的是( )
| A、在1个标准大气压下,水加热到100℃沸腾 |
| B、掷一枚硬币,正面朝下 |
| C、一个三角形三个内角的和小于180° |
| D、某运动员跳高的成绩是20.3米 |
 如图,要使△AFE∽△ABC,需要添加一个条件,请添加条件并给出证明过程.
如图,要使△AFE∽△ABC,需要添加一个条件,请添加条件并给出证明过程.