题目内容
已知函数y=x2-mx-m-3.
(1)求证:无论m为何值,此二次函数的图象与x轴都有两个不同的交点;
(2)若函数y的最小值为-2,求已知函数的表达式.
(1)求证:无论m为何值,此二次函数的图象与x轴都有两个不同的交点;
(2)若函数y的最小值为-2,求已知函数的表达式.
考点:抛物线与x轴的交点,待定系数法求二次函数解析式
专题:
分析:(1)计算出△的表达式,计算出其值为正数即可证明;
(2)利用顶点坐标公式解答.
(2)利用顶点坐标公式解答.
解答:解:(1)∵△=m2-4(-m-3)=m2+4m+12=m2+4m+4+8=(m+2)2+8>0,
∴无论m为何值,此二次函数的图象与x轴都有两个不同的交点;
(2)∵函数y的最小值为-2,
∴
=-2,
∴m1=m2=-2,
∴y=x2+2x-1.
∴无论m为何值,此二次函数的图象与x轴都有两个不同的交点;
(2)∵函数y的最小值为-2,
∴
| 4×1×(-m-3)-m2 |
| 4 |
∴m1=m2=-2,
∴y=x2+2x-1.
点评:本题考查了抛物线与x轴的交点及二次函数的顶点坐标公式,有一定难度.

练习册系列答案
相关题目
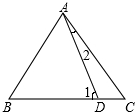 如图,已知AB=AC=BD,那么( )
如图,已知AB=AC=BD,那么( )| A、∠1=∠2 |
| B、2∠1+∠2=180° |
| C、∠1+3∠2=180° |
| D、3∠1-∠2=180° |
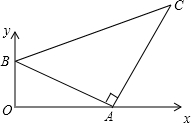 如图,直线AB分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,点A的坐标为(4,0),点B的坐标为(0,2),求C点的坐标.
如图,直线AB分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,点A的坐标为(4,0),点B的坐标为(0,2),求C点的坐标. 如图,已知直线y=-x+4与反比例函数y=
如图,已知直线y=-x+4与反比例函数y= 如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.
如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.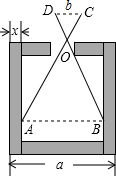 如图,已知零件的外径a=35cm,要求它的厚度x,需先求出内孔的直径AB,但不能直接量出AB,现用一个交叉卡钳(两条尺长AC和BD相等)测量,已知OA:OC=OB:OD=3,且量得CD=10cm,求厚度x.
如图,已知零件的外径a=35cm,要求它的厚度x,需先求出内孔的直径AB,但不能直接量出AB,现用一个交叉卡钳(两条尺长AC和BD相等)测量,已知OA:OC=OB:OD=3,且量得CD=10cm,求厚度x.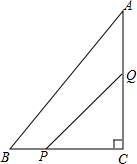 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,一动点P从点B出发,沿BC方向以1cm/s的速度向C移动,另一动点Q从点C出发,沿CA方向以2cm/s的速度向点A移动,点P、Q同时开始移动多少时间后,△CPQ与△CAB相似?
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,一动点P从点B出发,沿BC方向以1cm/s的速度向C移动,另一动点Q从点C出发,沿CA方向以2cm/s的速度向点A移动,点P、Q同时开始移动多少时间后,△CPQ与△CAB相似?