题目内容
 如图,已知直线y=-x+4与反比例函数y=
如图,已知直线y=-x+4与反比例函数y=| k |
| x |
(1)求a的值;
(2)求反比例函数的表达式;
(3)求△AOB的面积;
(4)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)直接利用待定系数法把A(-2,a)代入函数关系式y=-x+4中即可求出a的值;
(2)由(1)得到A点坐标后,把A点坐标代入反比例函数关系式y=
,即可得到答案;
(3)根据题意画出图象,过A点作AD⊥x轴于D,根据A的坐标求出AD的长,再根据B点坐标求出OB的长,根据三角形面积公式即可算出△AOB的面积;
(4)观察图象,一次函数在反比例函数图象上方的部分对应x的取值即为所求.
(2)由(1)得到A点坐标后,把A点坐标代入反比例函数关系式y=
| k |
| x |
(3)根据题意画出图象,过A点作AD⊥x轴于D,根据A的坐标求出AD的长,再根据B点坐标求出OB的长,根据三角形面积公式即可算出△AOB的面积;
(4)观察图象,一次函数在反比例函数图象上方的部分对应x的取值即为所求.
解答:解:(1)∵点A(-2,a)在y=-x+4的图象上,
∴a=2+4=6;
(2)将A(-2,6)代入y=
,得k=-12,
所以反比例函数的解析式为y=-
;
(3)如图:过A点作AD⊥x轴于D,
 ∵A(-2,6),
∵A(-2,6),
∴AD=6,
在直线y=-x+4中,令y=0,得x=4,
∴B(4,0),
∴OB=4,
∴△AOB的面积S=
OB×AD=
×4×6=12.
△AOB的面积为12;
(4)设一次函数与反比例函数的另一个交点为C,
把y=-x+4代入y=-
,
整理得x2-4x-12=0,
解得x=6或-2,
当x=6时,y=-6+4=-2,
所以C点坐标(6,-2),
由图象知,要使一次函数的值大于反比例函数的值,x的取值范围是:x<-2或0<x<6.
∴a=2+4=6;
(2)将A(-2,6)代入y=
| k |
| x |
所以反比例函数的解析式为y=-
| 12 |
| x |
(3)如图:过A点作AD⊥x轴于D,
 ∵A(-2,6),
∵A(-2,6),∴AD=6,
在直线y=-x+4中,令y=0,得x=4,
∴B(4,0),
∴OB=4,
∴△AOB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
△AOB的面积为12;
(4)设一次函数与反比例函数的另一个交点为C,
把y=-x+4代入y=-
| 12 |
| x |
整理得x2-4x-12=0,
解得x=6或-2,
当x=6时,y=-6+4=-2,
所以C点坐标(6,-2),
由图象知,要使一次函数的值大于反比例函数的值,x的取值范围是:x<-2或0<x<6.
点评:此题考查了反比例函数与一次函数的交点问题,待定系数法求函数关系式以及求三角形的面积,关键是求出A点坐标,利用数形结合的思想解决问题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,已知一次函数与反比例函数交于点A(-4,-2)和B(a,4),求反比例函数解析式和点B的坐标.
如图,已知一次函数与反比例函数交于点A(-4,-2)和B(a,4),求反比例函数解析式和点B的坐标. 如图,A、B、C为⊙O上三点,且
如图,A、B、C为⊙O上三点,且
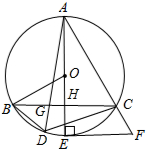 如图,AE为⊙O的直径,EF为⊙O的切线,E为切点,连接AF交⊙O于点C,CB∥EF交AE于H交⊙O于B,D为BC弧上一点,连接AD交BC于G.
如图,AE为⊙O的直径,EF为⊙O的切线,E为切点,连接AF交⊙O于点C,CB∥EF交AE于H交⊙O于B,D为BC弧上一点,连接AD交BC于G.