题目内容
 如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.
如图,已知直线AB分别与x轴、y轴交于点B、点A,且经过(2,-2)和(-1,4)两点,将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,求直线CD的函数解析式.考点:一次函数图象与几何变换
专题:
分析:先求出直线AB的解析式,再根据平移的性质求直线CD的解析式.
解答:解:设直线AB的解析式为y=kx+b,把A(2,-2)、点B(-1,4)代入得
,
解得
,
故直线AB的解析式为y=-2x+2;
将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC时,因为平移后的图形与原图形平行,
故平移以后的函数解析式为:y=-2x-2.
|
解得
|
故直线AB的解析式为y=-2x+2;
将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D,使DB=DC时,因为平移后的图形与原图形平行,
故平移以后的函数解析式为:y=-2x-2.
点评:本题要注意利用一次函数的特点,列出方程组,求出未知数的值从而求得其解析式;
求直线平移后的解析式时要注意平移时k的值不变,只有b发生变化.
求直线平移后的解析式时要注意平移时k的值不变,只有b发生变化.

练习册系列答案
相关题目
 如图,线段BD=
如图,线段BD= 已知平面内有A,B,C,D四点(如图),请画出直线AB,射线AC,射线DA,线段BD,线段DC,并标出线段BD与射线AC的交点P.
已知平面内有A,B,C,D四点(如图),请画出直线AB,射线AC,射线DA,线段BD,线段DC,并标出线段BD与射线AC的交点P.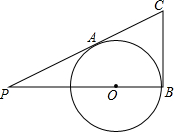 如图,PC切⊙O于点A,PO的延长线交⊙O于点B,BC切⊙O于点B,若CB:PC=1:2,则PO:OB是多少?
如图,PC切⊙O于点A,PO的延长线交⊙O于点B,BC切⊙O于点B,若CB:PC=1:2,则PO:OB是多少?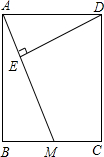 如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.
如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.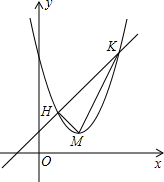 如图,抛物线y=x2-4x+5顶点为M,平移直线y=x交抛物线于点H、K,若S△MHK=3,求平移后直线的解析式.
如图,抛物线y=x2-4x+5顶点为M,平移直线y=x交抛物线于点H、K,若S△MHK=3,求平移后直线的解析式.