题目内容
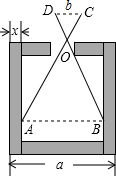 如图,已知零件的外径a=35cm,要求它的厚度x,需先求出内孔的直径AB,但不能直接量出AB,现用一个交叉卡钳(两条尺长AC和BD相等)测量,已知OA:OC=OB:OD=3,且量得CD=10cm,求厚度x.
如图,已知零件的外径a=35cm,要求它的厚度x,需先求出内孔的直径AB,但不能直接量出AB,现用一个交叉卡钳(两条尺长AC和BD相等)测量,已知OA:OC=OB:OD=3,且量得CD=10cm,求厚度x.考点:相似三角形的应用
专题:
分析:求出△AOB和△COD相似,利用相似三角形对应边成比例列式计算求出AB,再根据外径a的长度解答.
解答:解:∵OA:OC=OB:OD=3,∠AOB=∠COD,
∴△AOB∽△COD,
∴AB:CD=3,
即AB:10=3,
解得AB=30,
∵外径a=35cm,
∴30+2x=35,
解得x=2.5cm.
∴△AOB∽△COD,
∴AB:CD=3,
即AB:10=3,
解得AB=30,
∵外径a=35cm,
∴30+2x=35,
解得x=2.5cm.
点评:本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,熟记性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知关于x的一元二次方程x2-(2k+1)x+k2+2k=0有两个实数根x1,x2,使x1•x2-x12-x22≥0成立,则k的值为( )
| A、-1 | B、1 |
| C、大于等于1 | D、不存在 |
下列图形中,不是中心对称是( )
A、 |
B、 |
C、 |
D、 |
 如图,A、B、C为⊙O上三点,且
如图,A、B、C为⊙O上三点,且
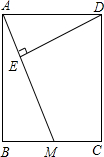 如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.
如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.