题目内容
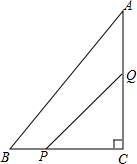 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,一动点P从点B出发,沿BC方向以1cm/s的速度向C移动,另一动点Q从点C出发,沿CA方向以2cm/s的速度向点A移动,点P、Q同时开始移动多少时间后,△CPQ与△CAB相似?
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,一动点P从点B出发,沿BC方向以1cm/s的速度向C移动,另一动点Q从点C出发,沿CA方向以2cm/s的速度向点A移动,点P、Q同时开始移动多少时间后,△CPQ与△CAB相似?考点:相似三角形的判定
专题:几何动点问题
分析:设运动时间为ts,则可知BP=t,CP=6-t,CQ=2t,当△CPQ和△CAB相似时,可知∠CPQ=∠B或∠CPQ=∠A,则有
=
或
=
,分别代入可得到关于t的方程,可求得t的值.
| CP |
| CB |
| CQ |
| CA |
| CP |
| CA |
| CQ |
| CB |
解答:解:设运动时间为ts,则BP=t,CP=6-t,CQ=2t,
∵∠PCQ=∠ACB=90°,
∴当△CPQ和△CAB相似时,有∠CPQ=∠B或∠CPQ=∠A,
当∠CPQ=∠B时,则有
=
,即
=
,解得t=2.4;
当∠CPQ=∠A时,则有
=
,即
=
,解得t=
.
综上可知当点P、Q同时运动2.4秒或
秒后,△CPQ和△CAB相似.
∵∠PCQ=∠ACB=90°,
∴当△CPQ和△CAB相似时,有∠CPQ=∠B或∠CPQ=∠A,
当∠CPQ=∠B时,则有
| CP |
| CB |
| CQ |
| CA |
| 6-t |
| 6 |
| 2t |
| 8 |
当∠CPQ=∠A时,则有
| CP |
| CA |
| CQ |
| CB |
| 6-t |
| 8 |
| 2t |
| 6 |
| 18 |
| 11 |
综上可知当点P、Q同时运动2.4秒或
| 18 |
| 11 |
点评:本题主要考查相似三角形的判定和性质,只有相似没有对应时应分情况讨论.注意方程思想的运用,用时间表示出线段的长度,化动为静是解决这类问题的思路.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
下列图形中,不是中心对称是( )
A、 |
B、 |
C、 |
D、 |
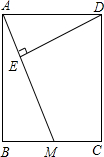 如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.
如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.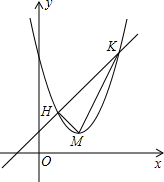 如图,抛物线y=x2-4x+5顶点为M,平移直线y=x交抛物线于点H、K,若S△MHK=3,求平移后直线的解析式.
如图,抛物线y=x2-4x+5顶点为M,平移直线y=x交抛物线于点H、K,若S△MHK=3,求平移后直线的解析式.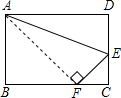 如图,一张长方形纸片宽AB=8cm,长BC=10cm,现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),则EC=
如图,一张长方形纸片宽AB=8cm,长BC=10cm,现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),则EC=