题目内容
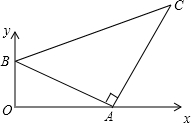 如图,直线AB分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,点A的坐标为(4,0),点B的坐标为(0,2),求C点的坐标.
如图,直线AB分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,点A的坐标为(4,0),点B的坐标为(0,2),求C点的坐标.考点:全等三角形的判定与性质,坐标与图形性质,等腰直角三角形
专题:
分析:过点C作CD⊥x轴,垂足为D,先证明△AOB≌△CDA,得出AD和CD的长,即可得出C点的坐标.
解答: 解:过点C作CD⊥x轴,垂足为D,
解:过点C作CD⊥x轴,垂足为D,
∴∠ADC=90°,
∴∠OAB+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠OAB=∠ACD,
∵OA=2,OB=2,
∴在△AOB和△CDA中,
,
∴△AOB≌△CDA(ASA),
∴AD=OB=2,CD=OA=4,
∴C点的坐标(6,4).
 解:过点C作CD⊥x轴,垂足为D,
解:过点C作CD⊥x轴,垂足为D,∴∠ADC=90°,
∴∠OAB+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠OAB=∠ACD,
∵OA=2,OB=2,
∴在△AOB和△CDA中,
|
∴△AOB≌△CDA(ASA),
∴AD=OB=2,CD=OA=4,
∴C点的坐标(6,4).
点评:本题考查了全等三角形的判定和性质,判断三角形全等的方法:SSS,SAS,ASA,AAS,还有直角三角形的特殊判断方法:HL.

练习册系列答案
相关题目
 如图,线段BD=
如图,线段BD= 已知平面内有A,B,C,D四点(如图),请画出直线AB,射线AC,射线DA,线段BD,线段DC,并标出线段BD与射线AC的交点P.
已知平面内有A,B,C,D四点(如图),请画出直线AB,射线AC,射线DA,线段BD,线段DC,并标出线段BD与射线AC的交点P.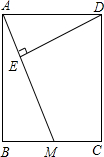 如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.
如图,已知矩形ABCD中,AB=12cm,BC=10cm,M是BC的中点,DE⊥AM于E,求DE的长.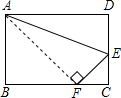 如图,一张长方形纸片宽AB=8cm,长BC=10cm,现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),则EC=
如图,一张长方形纸片宽AB=8cm,长BC=10cm,现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),则EC=