题目内容
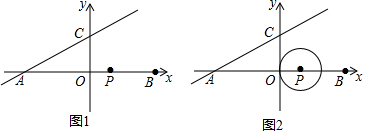
14.如图1,已知点A的坐标为(-5,0),点B与点A关于y轴对称,点C的坐标为(0,3),点P从点B出发,沿射线BA以每秒1个单位的速度运动,设点P运动时间为t秒.(1)点P的坐标为(5-t,0).(用含t的代数式表示)
(2)如图2,以点P为圆心,PO为半径画⊙P,当⊙P与直线AC相切时,求出t的值.
(3)如图3,若点Q以与点P相同的速度,同时从点A出发向点B方向运动,当点Q到达B时,以同样的速度返回向点A运动,当点Q到达A点时P,Q同时停止运动,过点Q作直线QT⊥x轴,交直线AC于点T,连接PT,BT.问在点P、Q运动过程中是否存在t使得△PBT为以PT为腰的等腰三角形?若存在,求出t的值;若不存在,请说明理由.
分析 (1)根据题意求出OP的长即可解决问题.
(2)如图2中,作BT⊥AC于T,设⊙P与AC相切于点H,连接PH.求出BT,首先判断在点O的右侧不存在⊙P与AC相切的情形,由PH∥BT,可得$\frac{PH}{BT}$=$\frac{AP}{AB}$,右侧列出方程求解即可.
(3)分三种情形求解①如图3中,当P、Q都在线段AB上运动时,由题意PB=t,PT=$\sqrt{Q{T}^{2}+P{Q}^{2}}$=$\sqrt{(\frac{3}{5}t)^{2}+(10-2t)^{2}}$,当PT=PB时,则有($\frac{3}{5}$t)2+(10-t)2=t2,解方程即可.②如图4中,当TP=TB时,易知QB=PQ.右侧列出方程即可.③如图5中,当点P在线段BA的延长线上时,由题意PQ=10,TQ=6,PT=$\sqrt{1{0}^{2}+{6}^{2}}$=2$\sqrt{34}$,只有PT=PB时,满足条件,由此即可解决问题.
解答 解:(1)∵B(5,0),PB=t,
∴OP=|5-t|,
∴P(5-t,0).
故答案为(5-t,0)
(2)如图2中,作BT⊥AC于T,设⊙P与AC相切于点H,连接PH.
在Rt△AOC中,∵OA=5,OC=3,
∴AC=$\sqrt{{5}^{2}+{3}^{2}}$=$\sqrt{34}$,
∵∠OAC=∠BAT,∠AOC=∠ATB,
∴△AOC∽△ATB,
∴$\frac{OC}{TB}$=$\frac{AC}{AB}$,
∴$\frac{3}{BT}$=$\frac{\sqrt{34}}{10}$,
∴BT=$\frac{15\sqrt{34}}{17}$>5,
∴BT>OB,
∴在点O的右侧不存在⊙P与AC相切的情形,
∵PH∥BT,
∴$\frac{PH}{BT}$=$\frac{AP}{AB}$,
∴$\frac{t-5}{\frac{15\sqrt{34}}{17}}$=$\frac{10-t}{10}$,
解得t=$\frac{16+3\sqrt{34}}{5}$.
(3)①如图3中,当P、Q都在线段AB上运动时,
由题意PB=t,PT=$\sqrt{Q{T}^{2}+P{Q}^{2}}$=$\sqrt{(\frac{3}{5}t)^{2}+(10-2t)^{2}}$,
当PT=PB时,则有($\frac{3}{5}$t)2+(10-t)2=t2,
解得t=$\frac{25}{7}$s或$\frac{25}{3}$s.
②如图4中,当TP=TB时,易知QB=PQ.
则有2t-10=10-t,
解得t=$\frac{20}{3}$s.
③如图5中,当点P在线段BA的延长线上时,
由题意PQ=10,TQ=6,PT=$\sqrt{1{0}^{2}+{6}^{2}}$=2$\sqrt{34}$,
只有PT=PB时,满足条件,
则有t=PB=2$\sqrt{34}$s,
综上所述,当△PBT为以PT为腰的等腰三角形时,t的值为$\frac{25}{7}$s或$\frac{25}{3}$s或$\frac{20}{3}$s或2$\sqrt{34}$s.
点评 本题考查圆综合题、切线的判定和性质、等腰三角形的判定和性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会把问题转化为方程解决,属于中考压轴题.

 如图,在直角坐标系中,直线y=-x+b与函数y=$\frac{k}{x}$的图象相交于点A、B,已知点A的坐标为(3,4),则△AOB的周长为( )
如图,在直角坐标系中,直线y=-x+b与函数y=$\frac{k}{x}$的图象相交于点A、B,已知点A的坐标为(3,4),则△AOB的周长为( )| A. | 10 | B. | 20 | C. | 10+2$\sqrt{2}$ | D. | 10+$\sqrt{2}$ |
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
| A. | a5 | B. | a9 | C. | a6 | D. | a-1 |
| A. | -3≤m<-2 | B. | -3<m≤-2 | C. | -3≤m≤-2 | D. | -3<m<-2 |
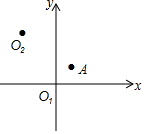 如图,在平面直角坐标系xO1y中,点A的坐标为(1,1).如果将x轴向上平移3个单位长度,将y轴向左平移2个单位长度,交于点O2,点A的位置不变,那么在平面直角坐标系xO2y中,点A的坐标是( )
如图,在平面直角坐标系xO1y中,点A的坐标为(1,1).如果将x轴向上平移3个单位长度,将y轴向左平移2个单位长度,交于点O2,点A的位置不变,那么在平面直角坐标系xO2y中,点A的坐标是( )| A. | (3,-2) | B. | (-3,2) | C. | (-2,-3) | D. | (3,4) |