题目内容
9.已知三角形三条边分别是1、$\sqrt{3}$、2,则该三角形为( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
分析 根据勾股定理的逆定理判断即可.
解答 解:∵12+($\sqrt{3}$)2=22,
∴以1,$\sqrt{3}$,2为边能组成直角三角形,
故选B.
点评 本题考查了勾股定理的逆定理,能熟记勾股定理的逆定理的内容是解此题的关键.

练习册系列答案
相关题目
20.如果-$\frac{2}{3}\sqrt{6-3x}$是二次根式,那么x应满足的条件是( )
| A. | x≥0 | B. | x≥2 | C. | x≤2 | D. | x<6 |
1.一个直角三角形的两直角边长分别为5和12,则它斜边上的高长为( )
| A. | 13 | B. | $\frac{13}{2}$ | C. | $\frac{60}{13}$ | D. | $\frac{12}{5}$ |
19.已知一组数据:5,7,4,8,6,7,2,则它的众数及中位数分别为( )
| A. | 7,8 | B. | 7,6 | C. | 6,7 | D. | 7,4 |
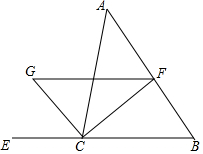 如图,CF是∠ACB的平分线,CG是∠ACB外角的平分线,FG∥BC交CG于点G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度数.
如图,CF是∠ACB的平分线,CG是∠ACB外角的平分线,FG∥BC交CG于点G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度数.
 如图,在等边三角形ABC中,点D、点E分别为AB,AC上的点,BE与CD相交于点F,BF=4EF=4,CE=AD.则S△AEB=5$\sqrt{3}$.
如图,在等边三角形ABC中,点D、点E分别为AB,AC上的点,BE与CD相交于点F,BF=4EF=4,CE=AD.则S△AEB=5$\sqrt{3}$.