题目内容
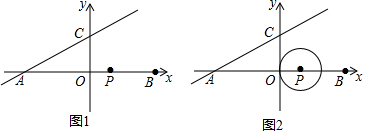
5. 如图,在直角坐标系中,直线y=-x+b与函数y=$\frac{k}{x}$的图象相交于点A、B,已知点A的坐标为(3,4),则△AOB的周长为( )
如图,在直角坐标系中,直线y=-x+b与函数y=$\frac{k}{x}$的图象相交于点A、B,已知点A的坐标为(3,4),则△AOB的周长为( )| A. | 10 | B. | 20 | C. | 10+2$\sqrt{2}$ | D. | 10+$\sqrt{2}$ |
分析 把A坐标代入确定出一次函数与反比例函数解析式,联立求出B的坐标,进而求出OA,OB,AB的长,即可确定出周长.
解答 解:把A(3,4)代入y=-x+b中得:b=7,即一次函数为y=-x+7;
代入y=$\frac{k}{x}$中得:k=12,即反比例函数为y=$\frac{12}{x}$,
联立得:$\left\{\begin{array}{l}{y=-x+7}\\{y=\frac{12}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$,即B(4,3),
根据勾股定理及两点间的距离公式得:OA=OB=5,AB=$\sqrt{2}$,
则△AOB周长为10+$\sqrt{2}$,
故选D
点评 此题考查了反比例函数与一次函数的交点问题,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.如果-$\frac{2}{3}\sqrt{6-3x}$是二次根式,那么x应满足的条件是( )
| A. | x≥0 | B. | x≥2 | C. | x≤2 | D. | x<6 |
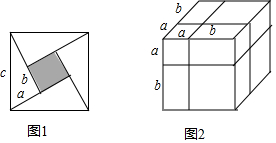 【知识生成】我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.
【知识生成】我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.