题目内容
4.已知:x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,求代数式x2+2xy+y2的值.分析 首先利用因式分解把x2+2xy+y2化为(x+y)2,然后再代入x、y的值进行计算即可.
解答 解:∵x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,
∴原式=(x+y)2,
=($\sqrt{3}+$1+$\sqrt{3}$-1)2,
=(2$\sqrt{3}$)2,
=12.
点评 此题主要考查了二次根式的化简计算,关键是正确把x2+2xy+y2进行因式分解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14.方程x+y+z+w=xyzw的正整数解的个数为( )
| A. | 0 | B. | 1 | C. | 12 | D. | 24 |
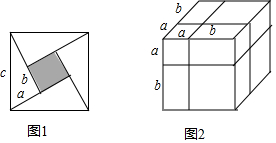 【知识生成】我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.
【知识生成】我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.