题目内容
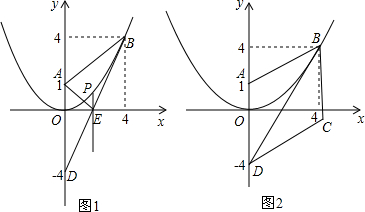
8.在平面直角坐标系中,点A的坐标为(0,1),抛物线y=ax2+bx+c的顶点为坐标原点O,且与直线y=2x-4有唯一交点B.(1)抛物线的函数表达式为y=$\frac{1}{4}$x2;
(2)如图1,设直线y=2x-4与y轴交于点D,点P是抛物线上一点.
①过点P作PE∥y轴,交直线BD于点E,若△ADE与△ABD相似,求点P的坐标;
②将△ABD沿直线BD折叠后,点A落在点C处(图2),是否存在点P,使得S△PCD=3S△PAB?如果存在,请求出所有满足条件的点P的坐标;如果不存在,请说明理由.
分析 (1)抛物线y=ax2+bx+c的顶点为坐标原点O,则b=c=0,与直线y=2x-4有唯一交点B,则根据根的判别式即可求解;
(2)求得D的坐标,利用三角形相似,则E的坐标即可求得,进而求得P的坐标;
(3)首先求得C的坐标,证明AB与CD平行且相等,则P在经过点(0,-$\frac{1}{4}$)且平行于AB的直线上,求得直线的解析式,然后解方程求解.
解答 解:(1)抛物线y=ax2+bx+c的顶点为坐标原点O,则b=c=0,
根据题意得:ax2=2x-4,
即ax2-2x+4=0,
△=4-16a=0,
解得:a=$\frac{1}{4}$,
则抛物线的解析式是:y=$\frac{1}{4}$x2;
(2)①在y=2x-4中,令x=0,解得:y=-4,则D的坐标是(0,-4).
解方程组$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}}\\{y=2x-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,
则B的坐标是(4,4).
由于△ADE与△ABD相似,那么只可能是△ADE∽△BDA,作图可知E在BD线段上,
则有$\frac{AD}{BD}=\frac{DE}{AD}$,设E(x,2x-4),则有DE=$\sqrt{{x}^{2}+(2x-4-(-4))^{2}}$=$\sqrt{5}x$;
又易求BD=$4\sqrt{5}$,AD=5;
故由AD2=BD×DE可求得x=$\frac{5}{4}$,再将x=$\frac{5}{4}$代入抛物线方程求得y=$\frac{25}{64}$;
即P点的坐标为($\frac{5}{4}$,$\frac{25}{64}$).
②设经过点A与BD垂直的直线的解析式是y=-$\frac{1}{2}$x+c,
把(0,1)代入得:c=1,则解析式是y=-$\frac{1}{2}$x+1,
设C的坐标是(m,-$\frac{1}{2}$m+1),则AC的中点坐标是($\frac{m}{2}$,$\frac{-\frac{1}{2}m+1+1}{2}$),即($\frac{m}{2}$,-$\frac{1}{4}$m+1),代入y=2x-4得:m-4=-$\frac{1}{4}$m+1,
解得:m=4.
则C的坐标是(4,-1).
作BN⊥y轴于点N,作CM⊥y轴于点M.则M的坐标是(0,-1),N的坐标是(0,4).
则在直角△ABN和直角△DCM中,
$\left\{\begin{array}{l}{BN=CM}\\{AN=DM}\end{array}\right.$,
∴直角△ABN≌直角△DCM(HL),
∴∠BAN=∠CDM,AB=CD,
∴AB∥CD.
∵S△PCD=3S△PAB,
在线段AD上的点E,使DE=3AE,则E的坐标是(0,-$\frac{1}{4}$),
设AB的解析式是y=mx+n,根据题意得:$\left\{\begin{array}{l}{n=1}\\{4m+n=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{n=1}\\{m=\frac{3}{4}}\end{array}\right.$,
则经过(0,-$\frac{1}{4}$)且平行与AB的直线的解析式是y=$\frac{3}{4}$x-$\frac{1}{4}$,
解方程组$\left\{\begin{array}{l}{y=\frac{3}{4}x-\frac{1}{4}}\\{y=\frac{1}{4}{x}^{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{3+\sqrt{5}}{2}}\\{y=\frac{7+3\sqrt{5}}{8}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{3-\sqrt{5}}{2}}\\{y=\frac{7-3\sqrt{5}}{8}}\end{array}\right.$,
则P的坐标是($\frac{3+\sqrt{5}}{2}$,$\frac{7+3\sqrt{5}}{8}$)或($\frac{3-\sqrt{5}}{2}$,$\frac{7-3\sqrt{5}}{8}$).
在DA的延长线上,到D和A的距离是1:3的点是(0,$\frac{7}{2}$),
则过(0,$\frac{7}{2}$)且平行与AB的直线的解析式是y=$\frac{3}{4}$x+$\frac{7}{2}$.
解方程组$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{7}{2}}\\{y=\frac{1}{4}{x}^{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{3+\sqrt{65}}{2}}\\{y=\frac{37+3\sqrt{65}}{8}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{3-\sqrt{65}}{2}}\\{y=\frac{37-3\sqrt{65}}{8}}\end{array}\right.$,
则P的坐标是($\frac{3+\sqrt{65}}{2}$,$\frac{37+3\sqrt{65}}{8}$)或($\frac{3-\sqrt{65}}{2}$,$\frac{37-3\sqrt{65}}{8}$).
总之,P的坐标是($\frac{3+\sqrt{5}}{2}$,$\frac{7+3\sqrt{5}}{8}$)或($\frac{3-\sqrt{5}}{2}$,$\frac{7-3\sqrt{5}}{8}$)或($\frac{3+\sqrt{65}}{2}$,$\frac{37+3\sqrt{65}}{8}$)或($\frac{3-\sqrt{65}}{2}$,$\frac{37-3\sqrt{65}}{8}$).
法二②:如图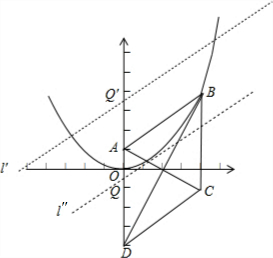
∵BC=AB=5=AD=CD,故易证四边形ABCD为菱形,
由于S△PCD=3S△PAB,AB∥CD且AB=CD,所以存在直线l上的所有点都符合题目要求,l∥AB∥CD,且l与CD的距离是l与AB距离的三倍;
设P点在直线y=$\frac{3}{4}$x+b上,且与y轴相交于Q点,当QD=3QA时,Q的坐标为(0,$-\frac{1}{4}$)或Q'(0,$\frac{7}{2}$);
求得l'的解析式为y=$\frac{3}{4}$x-$\frac{1}{4}$,联立抛物线方程解得:$\left\{\begin{array}{l}{x=\frac{3+\sqrt{5}}{2}}\\{y=\frac{7+3\sqrt{5}}{8}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{3-\sqrt{5}}{2}}\\{y=\frac{7-3\sqrt{5}}{8}}\end{array}\right.$;
l''的解析式为y=$\frac{3}{4}$x+$\frac{7}{2}$,联立抛物线方程解得:$\left\{\begin{array}{l}{x=\frac{3+\sqrt{65}}{2}}\\{y=\frac{37+3\sqrt{65}}{8}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{3-\sqrt{65}}{2}}\\{y=\frac{37-3\sqrt{65}}{8}}\end{array}\right.$;
综上:P的坐标是($\frac{3+\sqrt{5}}{2}$,$\frac{7+3\sqrt{5}}{8}$)或($\frac{3-\sqrt{5}}{2}$,$\frac{7-3\sqrt{5}}{8}$)或($\frac{3+\sqrt{65}}{2}$,$\frac{37+3\sqrt{65}}{8}$)或($\frac{3-\sqrt{65}}{2}$,$\frac{37-3\sqrt{65}}{8}$).
点评 本题考查了待定系数法求函数的解析式,以及直线垂直和平行的条件,判断AB与CD平行且相等是解题的关键.

| A. | 13分钟 | B. | 14分钟 | C. | 15分钟 | D. | 16分钟 |
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
| A. | 甲需4天,乙需2天 | B. | 甲需3天,乙需1天 | C. | 甲需6天,乙需4天 | D. | 甲需5天,乙需3天 |
| A. | x1=2,x2=-1 | B. | x1=1,x2=-2 | C. | x1=3,x2=-2 | D. | x1=2,x2=-3 |
 已知:如图,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b(a≠0)的图象交于A(3,1)、B(m,-3)两点.
已知:如图,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b(a≠0)的图象交于A(3,1)、B(m,-3)两点. 如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.
如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.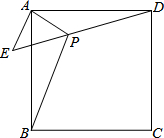 如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,EA=AP=1,且D、P、E三点共线,若PB=$\sqrt{5}$,则PC=$\sqrt{3}$.
如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,EA=AP=1,且D、P、E三点共线,若PB=$\sqrt{5}$,则PC=$\sqrt{3}$.