题目内容
13. 如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.
如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.(1)当t=1时,正方形EFGH的边长是3;当t=4时,正方形EFGH的边长是8;
(2)当0<t≤3时,求S与t的函数关系式.
分析 (1)当t=1时,根据PE=2t,PF=t即可求出EF的值,当t=4时,点E运动到点A后返回,PE=2AP-2t,PF=t,由此即可求出EF的值;
(2)当点H在线段AC上时,可求出t=$\frac{6}{5}$,可分两种情况讨论:当0<t≤$\frac{6}{5}$时,S=S正方形EFGH=EF2,只需用t的代数式表示出EF即可解决问题;当$\frac{6}{5}$<t≤3时,S=S五边形EFGMN=S正方形EFGH-S△MHN=EF2-$\frac{1}{2}$HN•HM,只需用t的代数式分别表示出EF、HN、HM即可解决问题.
解答 解:(1)当t=1时,PE=2×1=2,PF=1×1=1,EF=EP+PF=2+1=3.
当t=4时,PE=12-2×4=4,PF=1×4=4,EF=EP+PF=4+4=8.
故答案分别为:3、8;
(2)当点H在线段AC上时,
则有AE=HE=EF,即6-2t=3t,
解得:t=$\frac{6}{5}$.
①当0<t≤$\frac{6}{5}$时,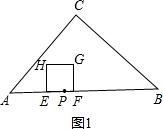
EF=EP+PF=2t+t=3t,
则S=9t2;
②当$\frac{6}{5}$<t≤3时,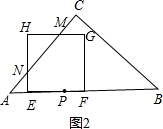
∵∠C=90°,AC=BC,
∴∠A=45°.
∵四边形EFGH是正方形,
∴HE=EF=3t,∠H=∠HEF=90°,
∴∠ANE=90°-45°=45°,
∴∠ANE=∠A=45°,
∴NE=AE=AP-EP=6-2t,
∴HN=HE-NE=3t-(6-2t)=5t-6.
∵∠HNM=∠ANE=45°,
∴∠HMN=90°-45°=45°,
∴∠HMN=∠HNM=45°,
∴HM=HN=5t-6,
∴S=S正方形EFGH-S△NHM
=(3t)2-$\frac{1}{2}$(5t-6)2
=-$\frac{7}{2}$t2+30t-18.
综上所述:S与t的函数关系式为
S=$\left\{\begin{array}{l}{9{t}^{2},0<t≤\frac{6}{5}}\\{-\frac{7}{2}{t}^{2}+30t-18,\frac{6}{5}<t≤3}\end{array}\right.$.
点评 本题主要考查了正方形的性质、等腰三角形的判定与性质、三角形的面积公式等知识,在解题的过程中用到了割补法、分类讨论的思想,准确分类是解决第(2)小题的关键.

 阅读快车系列答案
阅读快车系列答案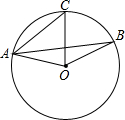 如图,在⊙O中,∠BAC=25°,则∠BOC的度数为( )
如图,在⊙O中,∠BAC=25°,则∠BOC的度数为( )| A. | 25° | B. | 50° | C. | 60° | D. | 80° |
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
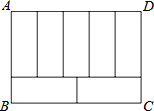 如图:周长为68的长方形ABCD被分成7个形状、大小完全一样的长方形,则ABCD的面积是多少?
如图:周长为68的长方形ABCD被分成7个形状、大小完全一样的长方形,则ABCD的面积是多少?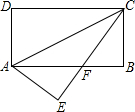 如图.在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点E处,且CE与AB交于F,那么S△ACF为( )
如图.在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点E处,且CE与AB交于F,那么S△ACF为( )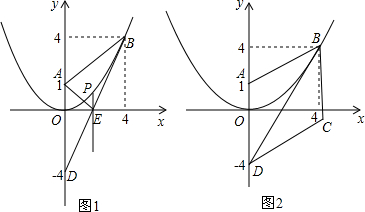
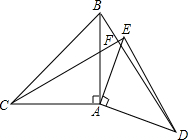 如图,已知△ABC和△ADE都是等腰直角三角形,∠1=∠2=90°,AB=AC,AD=AE.△ADE可以绕点A旋转.
如图,已知△ABC和△ADE都是等腰直角三角形,∠1=∠2=90°,AB=AC,AD=AE.△ADE可以绕点A旋转.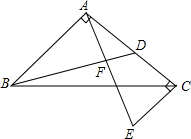 如图,在等腰直角三角形中,∠BAC=90°,AB=AC,点D是AC上一点,过点A作AF⊥BD,过点C作CE⊥AC的延长线于E,说明AE=BD.
如图,在等腰直角三角形中,∠BAC=90°,AB=AC,点D是AC上一点,过点A作AF⊥BD,过点C作CE⊥AC的延长线于E,说明AE=BD.