题目内容
20.为缓解甲、乙两地旱情,某水库计划向甲、乙两地送水,甲地需水量为180万立方米,乙地需电水量为120万立方米,现已两次送水:往甲地送水3天,乙地送水2天,共送水84万立方米;往甲地送水2天,乙地送水3天,共送水81万立方米,则完成往甲地,乙地送水任务还各需( )天.| A. | 甲需4天,乙需2天 | B. | 甲需3天,乙需1天 | C. | 甲需6天,乙需4天 | D. | 甲需5天,乙需3天 |
分析 可设往甲地每天送水x万立方米,往乙地每天送水y万立方米,根据等量关系:①往甲地送水3天,乙地送水2天,共送水84万立方米;②往甲地送水2天,乙地送水3天,共送水81万立方米;列出方程组求解即可.
解答 解:设往甲地每天送水x万立方米,往乙地每天送水y万立方米,依题意有
$\left\{\begin{array}{l}{3x+2y=84}\\{2x+3y=81}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=18}\\{y=15}\end{array}\right.$,
180÷18-3-2=5天.
120÷15-2-3=3天.
答:完成往甲地送水任务还需5天,完成往乙地送水任务还需3天.
故选:D.
点评 此题主要考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.

练习册系列答案
相关题目
10.若分式$\frac{x-2}{x}$的值为零,则x的值是( )
| A. | 0 | B. | 2 | C. | -2 | D. | 2或-2 |
15.已知关于x的方程x2-2x+m-1=0,若方程的一个根为1,则m的值是( )
| A. | -2 | B. | 2 | C. | 0 | D. | 1 |
12.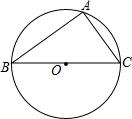 如图,已知AB是⊙O的直径,∠B=30°,则∠C的度数是( )
如图,已知AB是⊙O的直径,∠B=30°,则∠C的度数是( )
 如图,已知AB是⊙O的直径,∠B=30°,则∠C的度数是( )
如图,已知AB是⊙O的直径,∠B=30°,则∠C的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
9.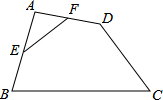 如图,在四边形ABCD中,E,F分别是AB,AD的中点.若EF=2,BC=5,CD=3,则sinC等于( )
如图,在四边形ABCD中,E,F分别是AB,AD的中点.若EF=2,BC=5,CD=3,则sinC等于( )
 如图,在四边形ABCD中,E,F分别是AB,AD的中点.若EF=2,BC=5,CD=3,则sinC等于( )
如图,在四边形ABCD中,E,F分别是AB,AD的中点.若EF=2,BC=5,CD=3,则sinC等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
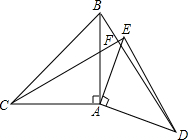
 如图,在△ABC中,AB=4,AC=3,AD、AE分别是△ABC角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
如图,在△ABC中,AB=4,AC=3,AD、AE分别是△ABC角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
 如图,已知△ABC和△ADE都是等腰直角三角形,∠1=∠2=90°,AB=AC,AD=AE.△ADE可以绕点A旋转.
如图,已知△ABC和△ADE都是等腰直角三角形,∠1=∠2=90°,AB=AC,AD=AE.△ADE可以绕点A旋转.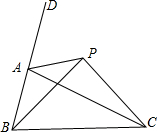 如图,点P是△ABC的外角∠DAC平分线上的一点,你能比较PB+PC与AB+AC的大小吗?说说你的理由.
如图,点P是△ABC的外角∠DAC平分线上的一点,你能比较PB+PC与AB+AC的大小吗?说说你的理由.