题目内容
4.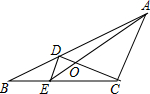 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:25 |
分析 根据相似三角形的判定定理得到△DOE∽△COA,根据相似三角形的性质定理得到$\frac{DE}{AC}$=$\frac{1}{5}$,$\frac{BE}{BC}$=$\frac{DE}{AC}$=$\frac{1}{5}$,结合图形得到$\frac{BE}{EC}$=$\frac{1}{4}$,得到答案.
解答 解:∵DE∥AC,
∴△DOE∽△COA,又S△DOE:S△COA=1:25,
∴$\frac{DE}{AC}$=$\frac{1}{5}$,
∵DE∥AC,
∴$\frac{BE}{BC}$=$\frac{DE}{AC}$=$\frac{1}{5}$,
∴$\frac{BE}{EC}$=$\frac{1}{4}$,
∴S△BDE与S△CDE的比是1:4,
故选:B.
点评 本题考查的是相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
15.计算(a-1)2正确的是( )
| A. | a2-a+1 | B. | a2-2a+1 | C. | a2-2a-1 | D. | a2-1 |
13.下列运算正确的是( )
| A. | a+2a=2a2 | B. | (-2ab2)2=4a2b4 | C. | a6÷a3=a2 | D. | (a-3)2=a2-9 |
 如图,抛物线y=ax2+bx-3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=-$\frac{1}{3}$x+1与y轴交于点D.
如图,抛物线y=ax2+bx-3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=-$\frac{1}{3}$x+1与y轴交于点D.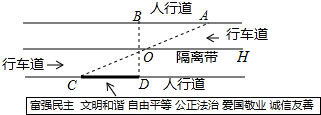
 如图,在?ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.
如图,在?ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.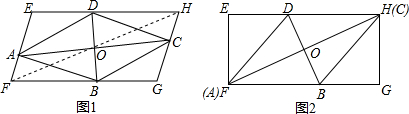
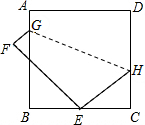 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )