题目内容
14.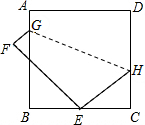 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据折叠可得DH=EH,在直角△CEH中,设CH=x,则DH=EH=9-x,根据BE:EC=2:1可得CE=3,可以根据勾股定理列出方程,从而解出CH的长.
解答  解:设CH=x,则DH=EH=9-x,
解:设CH=x,则DH=EH=9-x,
∵BE:EC=2:1,BC=9,
∴CE=$\frac{1}{3}$BC=3,
∴在Rt△ECH中,EH2=EC2+CH2,
即(9-x)2=32+x2,
解得:x=4,
即CH=4.
故选(B).
点评 本题主要考查正方形的性质以及翻折变换,折叠问题其实质是轴对称变换.在直角三角形中,利用勾股定理列出方程进行求解是解决本题的关键.

练习册系列答案
相关题目
4.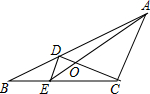 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:25 |
2.我国建造的长江三峡水电站,估计总装机容量达16780000千瓦,16780000用科学记数法表示为( )
| A. | 16.7×106 | B. | 1.68×107 | C. | 1.678×107 | D. | 1.678×108 |
9. 图中是一个少数名族手鼓的轮廓图,其主视图是( )
图中是一个少数名族手鼓的轮廓图,其主视图是( )
 图中是一个少数名族手鼓的轮廓图,其主视图是( )
图中是一个少数名族手鼓的轮廓图,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
4.关于x的分式方程$\frac{2x-m}{x+1}$=3的解是正数,则字母m的取值范围是( )
| A. | m>3 | B. | m<3 | C. | m>-3 | D. | m<-3 |
 昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.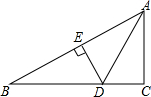 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=3,则DE的长为( )